
【题目】小明准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段围成一个正方形.
的铁丝剪成两段,并把每一段围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小明该怎么剪?
,小明该怎么剪?
(2)小刚对小明说:“这两个正方形的面积之和不可能等于![]() .”小刚的说法对吗?请说明理由.
.”小刚的说法对吗?请说明理由.
【答案】(1)剪成40cm和80cm的两段;(2)小刚的说法正确,理由见解析.
【解析】
(1)设剪成一段长为xcm,则另一段长为(120-x)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于500cm2建立方程求出其解即可;
(2)![]() ,如果方程有解就说明小刚的说法错误,否则正确.
,如果方程有解就说明小刚的说法错误,否则正确.
(1)设剪成一段长为xcm,则另一段长为(120-x)cm,依题意得
![]() ,
,
解得![]() ,
,![]() ,∴把一根120cm长的铁丝剪成40cm和80cm的两段,围成的正方形面积之和为500cm2;
,∴把一根120cm长的铁丝剪成40cm和80cm的两段,围成的正方形面积之和为500cm2;
(2)小刚的说法正确,因为![]() 整理得,
整理得,
![]() ,
,
∵△=-1600<0,
∴两个正方形的面积之和不可能等于400cm2,
∴小刚的说法正确.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,在一次购物中,张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.
(1)张华用“微信”支付的概率是______.
(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)
查看答案和解析>>
科目:初中数学 来源: 题型:
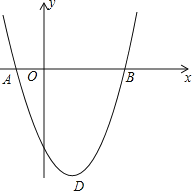
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,顶点为D.
两点,顶点为D.
![]() 求a和b的值;
求a和b的值;
![]() 将抛物线沿y轴方向上下平移,使顶点D落在x轴上.
将抛物线沿y轴方向上下平移,使顶点D落在x轴上.
![]() 求平移后所得图象的函数解析式;
求平移后所得图象的函数解析式;
![]() 若将平移后的抛物线,再沿x轴方向左右平移得到新抛物线,若
若将平移后的抛物线,再沿x轴方向左右平移得到新抛物线,若![]() 时,新抛物线对应的函数有最小值2,求平移的方向和单位长度.
时,新抛物线对应的函数有最小值2,求平移的方向和单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点P是△ABC内部的一个动点,且满足∠PBC=∠PCA,则线段AP长的最小值为( )
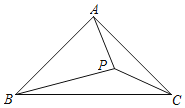
A.0.5B.![]() ﹣1C.2﹣
﹣1C.2﹣![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
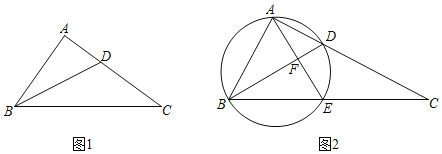
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 度;
(2)如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
①求证:△BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
(3)如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连结AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省每年的体育考试分成必考科目与选考科目两部分.其中选考科目是从一分钟跳绳、掷实心球、坐位体前屈、仰卧起坐四个项目中选取一项.王红与李丽是一对好朋友且都在2020年参加中考,实心球是她俩的弱项,其他三项都非常强,体育考试选考的四个项目中,她俩一定不会选实心球.
(1)王红在选考项目中,选中坐位体前屈的概率是 .
(2)王红与李丽选取同一个选考项目的概率是多少? (在画树状图或列表时,“一分钟跳绳"用“![]() ”表示,“坐位体前屈”用“
”表示,“坐位体前屈”用“![]() "表示,“仰卧起坐”用“
"表示,“仰卧起坐”用“![]() ”表示,“掷实心球”用“
”表示,“掷实心球”用“![]() ”表示)
”表示)
(3)通过对我省某市2020年参加中考的学生进行随机调查,发现该市选择“坐位体前屈”的学生的频率稳定在![]() 左右,已知该市有
左右,已知该市有![]() 人参加2020年中考体育,请由此估计该市这
人参加2020年中考体育,请由此估计该市这![]() 名学生中选择“坐位体前屈”的人数.
名学生中选择“坐位体前屈”的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
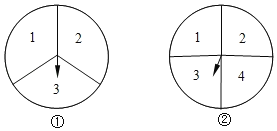
【题目】(1)甲、乙两人用如图所示的①、②两个转盘(分别三等分和四等分)做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙获胜.求甲获胜的概率.
(2)在一个不透明的袋中放入除颜色外都相同的1个红球和n个白球,搅匀后从中任意摸出2个球,若两个球中出现红球的概率与(1)中甲获胜的概率相同,则n= .
查看答案和解析>>
科目:初中数学 来源: 题型:
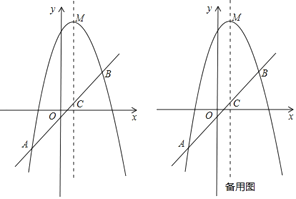
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
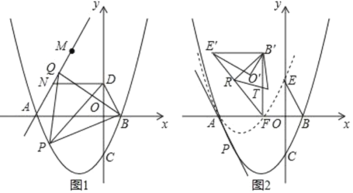
【题目】如图,在平面直角标系中,抛物线C:y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=![]() OC,连接BD,
OC,连接BD,
(1)如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+![]() AM的最小值
AM的最小值
(2)如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y=![]() 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com