
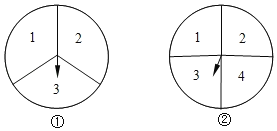
【题目】(1)甲、乙两人用如图所示的①、②两个转盘(分别三等分和四等分)做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙获胜.求甲获胜的概率.
(2)在一个不透明的袋中放入除颜色外都相同的1个红球和n个白球,搅匀后从中任意摸出2个球,若两个球中出现红球的概率与(1)中甲获胜的概率相同,则n= .
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
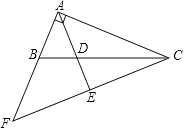
【题目】直角三角形ABC中,![]() ,D是斜边BC上一点,且
,D是斜边BC上一点,且![]() ,过点C作
,过点C作![]() ,交AD的延长线于点E,交AB延长线于点F.
,交AD的延长线于点E,交AB延长线于点F.
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,过点B作
,过点B作![]() 于点G,连接
于点G,连接![]() 依题意补全图形,并求四边形ABGD的面积.
依题意补全图形,并求四边形ABGD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段围成一个正方形.
的铁丝剪成两段,并把每一段围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小明该怎么剪?
,小明该怎么剪?
(2)小刚对小明说:“这两个正方形的面积之和不可能等于![]() .”小刚的说法对吗?请说明理由.
.”小刚的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地农产品专卖店收购了一种非常受欢迎的土特产,该店以![]() 元/千克收购了这种土特产
元/千克收购了这种土特产![]() 千克,若立即销往外地,每千克可以获利
千克,若立即销往外地,每千克可以获利![]() 元.根据市场调查发现,该种土特产的销售单价每天上涨
元.根据市场调查发现,该种土特产的销售单价每天上涨![]() 元/千克,为了获得更大利润,该店决定先贮藏一段时间后再出售.根据以往经验,这批土特产的贮藏时间不宜超过
元/千克,为了获得更大利润,该店决定先贮藏一段时间后再出售.根据以往经验,这批土特产的贮藏时间不宜超过![]() 天,在贮藏过程中平均每天损耗
天,在贮藏过程中平均每天损耗![]() 千克.
千克.
(1)若商家将这批土特产贮藏![]() 天后一次性出售,请完成下列表格:
天后一次性出售,请完成下列表格:
每千克土特产售价(单位:元) | 可供出售的土特产质量(单位:克) | |
现在出售 |
|
|
|
|
|
(2)将这批土特产贮藏多少天后一次性出售最终可获得总利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
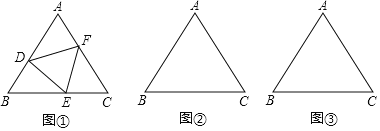
【题目】(概念提出)如图 ①,若正△DEF的三个顶点分别在正△ABC的边AB、BC、AC上,则我们称△DEF是正△ABC的内接正三角形.
(1)求证:△ADF≌△BED.
(问题解决)利用直尺和圆规作正三角形的内接正三角形(保留作图痕迹,不写作法).
(2)如图 ②,正△ABC的边长为a,作正△ABC的内接正△DEF,使△DEF的边长最短,并说明理由;
(3)如图③,作正△ABC的内接正△DEF,使FD⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其它方面完全相同,若背面朝上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面朝上方在桌面上,甲从中随机抽取一张卡片,记该卡片上的数字为![]() ,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为
,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为![]() ,组成一数对
,组成一数对![]() .
.
(1)请写出![]() .所有可能出现的结果;
.所有可能出现的结果;
(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽依次卡片,卡片上述资质和为奇数则甲赢,数字之和为偶数则乙赢,你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
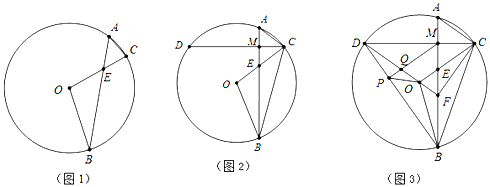
【题目】如图1,在![]() 中,弦
中,弦![]() 与半径
与半径![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 时,求线段
时,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省第十五届运动会乒乓球比赛于2018年8月13日上午在山西省体育博物馆的比赛场馆内正式拉开了帷幕.第十五届运动会竞技体育组乒乓球项目产生的决赛运动员名单中太原市共27人,其中甲组有甲、乙、丙、丁四名女子运动员,若进行一次乒乓球单打比赛,要通过抽签从中选出两名运动员打第一场比赛.
(1)若已确定甲打第一场,再从其余三名运动员中随机选取一位,求恰好选中乙的概率;
(2)若两名运动员都不确定,请用树状图法或列表法,求恰好选中甲、乙两名运动员的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com