
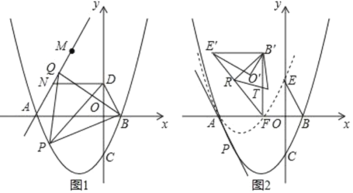
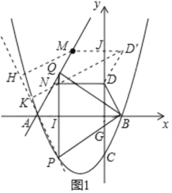
【题目】如图,在平面直角标系中,抛物线C:y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=![]() OC,连接BD,
OC,连接BD,
(1)如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+![]() AM的最小值
AM的最小值
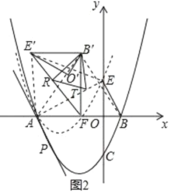
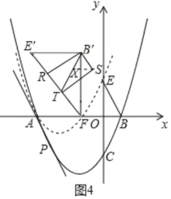
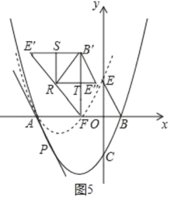
(2)如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y=![]() 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
【答案】解:(1)![]() ;(2)(
;(2)(![]() ,3+
,3+![]() )或(﹣
)或(﹣![]() ,
,![]() )或(﹣2,2
)或(﹣2,2![]() ).
).
【解析】
(1)由抛物线解析式求点A、B、C坐标,由OD=![]() OC求点D坐标.设点P横坐标为t,可用待定系数法求得用t表示的直线PB解析式,即能用t表示PB与y轴交点G的坐标,进而用t表示DG的长.以DG为界把△PBD分成左右两边的△PDG与△BDG,则以DG为底计算易求得△PBD面积与t的二次函数关系式,求对称轴即得到△PBD最大时t的值,进而得到点P坐标.求得∠ABP=30°,即x轴平分∠PBQ,故点P、Q关于x轴对称,得到点Q坐标,进而得到直线AQ解析式,发现∠QAB=∠PAB=60°.作直线AP,可得直线AQ与AP夹角为60°,过点M作MH⊥AP于H,即构造出特殊Rt△MAN,得到MH=
OC求点D坐标.设点P横坐标为t,可用待定系数法求得用t表示的直线PB解析式,即能用t表示PB与y轴交点G的坐标,进而用t表示DG的长.以DG为界把△PBD分成左右两边的△PDG与△BDG,则以DG为底计算易求得△PBD面积与t的二次函数关系式,求对称轴即得到△PBD最大时t的值,进而得到点P坐标.求得∠ABP=30°,即x轴平分∠PBQ,故点P、Q关于x轴对称,得到点Q坐标,进而得到直线AQ解析式,发现∠QAB=∠PAB=60°.作直线AP,可得直线AQ与AP夹角为60°,过点M作MH⊥AP于H,即构造出特殊Rt△MAN,得到MH=![]() AM.把点D平移到D',使DD'∥MN且DD'=MN,构造平行四边形MNDD',故DN=D'M.所以DN+MN+
AM.把点D平移到D',使DD'∥MN且DD'=MN,构造平行四边形MNDD',故DN=D'M.所以DN+MN+![]() AM可转化为MN+D'M+MH.易得当点D'、M、H在同一直线上时,线段和会最短,即过D'作D'K⊥AP于K,D'K的值为所求.根据平移性质求D'坐标,求直线D'K与直线AP解析式,联立方程组求得K的坐标,即求得D'K的长.
AM可转化为MN+D'M+MH.易得当点D'、M、H在同一直线上时,线段和会最短,即过D'作D'K⊥AP于K,D'K的值为所求.根据平移性质求D'坐标,求直线D'K与直线AP解析式,联立方程组求得K的坐标,即求得D'K的长.
(2)抛物线平移不改变开口方向和大小,再求得点E坐标和点A坐标,可用待定系数法求平移后的解析式,进而求得点F.由旋转性质可得△ABB'与△AEE'为等边三角形,求出点E'、B'坐标,B'F⊥x轴且△B'E'F为含30°的直角三角形.把点R从E'移动到F的过程,发现∠RB'T一定小于90°,不可能成为矩形内角,故只能是∠B'RT或∠B'TR=90°.点T可以在E'F上,也可以在B'F上,画出图形,根据含30°的直角三角形三边关系计算各线段长,即能求点S坐标.
解:(1)如图1,过点D作DD'∥MN,且DD'=MN=2,连接D'M;过点D'作D'J⊥y轴于点J;
作直线AP,过点M作MH⊥AP于点H,过点D'作D'K⊥AP于点K
∵y=![]() =0
=0
解得:x1=﹣3,x2=1
∴A(﹣3,0),B(1,0)
∵x=0时,y=![]() =﹣
=﹣![]()
∴C(0,﹣![]() ),OC=
),OC=![]()
∴OD=![]() OC=
OC=![]() ,D(0,
,D(0,![]() )
)
设P(t,![]() t2+
t2+![]() t﹣
t﹣![]() )(﹣3<t<1)
)(﹣3<t<1)
设直线PB解析式为y=kx+b,与y轴交于点G
∴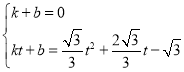 解得:
解得: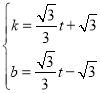
∴直线PB:y=(![]() t+
t+![]() )x﹣
)x﹣![]() t﹣
t﹣![]() ,G(0,﹣
,G(0,﹣![]() t﹣
t﹣![]() )
)
∴DG=![]() ﹣(﹣
﹣(﹣![]() t﹣
t﹣![]() )=
)=![]() t+
t+![]()
∴S△BPD=S△BDG+S△PDG=![]() DGxB+
DGxB+![]() DG|xP|=
DG|xP|=![]() DG(xB﹣xP)=
DG(xB﹣xP)=![]() (
(![]() t+
t+![]() )(1﹣t)=﹣
)(1﹣t)=﹣![]() (t2+4t﹣5)
(t2+4t﹣5)
∴t=﹣![]() =﹣2时,S△BPD最大
=﹣2时,S△BPD最大
∴P(﹣2,﹣![]() ),直线PB解析式为y=
),直线PB解析式为y=![]() x﹣
x﹣![]() ,直线AP解析式为y=﹣
,直线AP解析式为y=﹣![]() x﹣3
x﹣3![]()
∴tan∠ABP=![]() =
=![]()
∴∠ABP=30°
∵△BPQ为等边三角形
∴∠PBQ=60°,BP=PQ=BQ
∴BA平分∠PBQ
∴PQ⊥x轴,PQ与x轴交点I为PQ中点
∴Q(﹣2,![]() )
)
∴Rt△AQI中,tan∠QAI=![]()
∴∠QAI=∠PAI=60°
∴∠MAH=180°﹣∠PAI﹣∠QAI=60°
∵MH⊥AP于点H
∴Rt△AHM=90°,sin∠MAH=![]()
∴MH=![]() AM
AM
∵DD'∥MN,DD'=MN=2
∴四边形MNDD'是平行四边形
∴D'M=DN
∴DN+MN+![]() AM=2+D'M+MH
AM=2+D'M+MH
∵D'K⊥AP于点K
∴当点D'、M、H在同一直线上时,DN+MN+![]() AM=2+D'M+MH=2+D'K最短
AM=2+D'M+MH=2+D'K最短
∵DD'∥MN,D(0,![]() )
)
∴∠D'DJ=30°
∴D'J=![]() DD'=1,DJ=
DD'=1,DJ=![]() DD'=
DD'=![]()
∴D'(1,![]() )
)
∵∠PAI=60°,∠ABP=30°
∴∠APB=180°﹣∠PAI﹣∠ABP=90°
∴PB∥D'K
设直线D'K解析式为y=![]() x+d,
x+d,
把点D'代入得:![]() +d=
+d=![]()
解得:d=![]()
∴直线D'K:y=![]() x+
x+![]()
把直线AP与直线D'K解析式联立得:
 解得:
解得: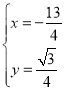
∴K(﹣![]() ,
,![]() )
)
∴D'K=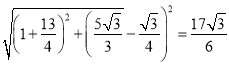
∴DN+MN+![]() AM的最小值为
AM的最小值为![]()
(2)连接B'A、BB'、EA、E'A、EE',如图2
∵点C(0,﹣![]() )关于x轴的对称点为E
)关于x轴的对称点为E
∴E(0,![]() )
)
∴tan∠EAB=![]()
∴∠EAB=30°
∵抛物线C'由抛物线C平移得到,且经过点E
∴设抛物线C'解析式为:y=![]() x2+mx+
x2+mx+![]()
∵抛物线C'经过点A(﹣3,0)
∴![]() ×9﹣3m+
×9﹣3m+![]() =0
=0
解得:m=![]()
∴抛物线C'解析式为:y=![]() x2+
x2+![]() x+
x+![]()
∵![]() x2+
x2+![]() x+
x+![]() =0,解得:x1=﹣3,x2=﹣1
=0,解得:x1=﹣3,x2=﹣1
∴F(﹣1,0)
∵将△BOE绕着点A逆时针旋转60°得到△B′O′E′
∴∠BAB'=∠EAE'=60°,AB'=AB=1﹣(﹣3)=4,AE'=AE=![]()
∴△ABB'、△AEE'是等边三角形
∴∠E'AB=∠E'AE+∠EAB=90°,点B'在AB的垂直平分线上
∴E'(﹣3,2![]() ),B'(﹣1,2
),B'(﹣1,2![]() )
)
∴B'E'=2,∠FB'E'=90°,E'F=![]()
∴∠B'FE'=30°,∠B'E'F=60°
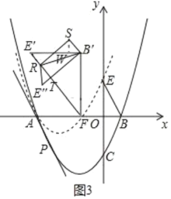
①如图3,点T在E'F上,∠B'TR=90°
过点S作SW⊥B'E'于点W,设翻折后点E'的对应点为E'
∴∠E'B'T=30°,B'T=![]() B'E'=
B'E'=![]()
∵△B′E′R翻折得△B'E'R
∴∠B'E'R=∠B'E'R=60°,B'E'=B'E'=2
∴E'T=B'E'﹣B'T=2﹣![]()
∴Rt△RTE'中,RT=![]() E'T=2
E'T=2![]() ﹣3
﹣3
∵四边形RTB'S是矩形
∴∠SB'T=90°,SB'=RT=2![]() ﹣3
﹣3
∴∠SB'W=∠SB'T﹣∠E'B'T=60°
∴B'W=![]() SB'=
SB'=![]() ﹣
﹣![]() ,SW=
,SW=![]() SB'=3﹣
SB'=3﹣![]()
∴xS=xB'﹣B'W=![]() ,yS=yB'+SW=3+
,yS=yB'+SW=3+
∴S(![]() ,3+
,3+![]() )
)
②如图4,点T在E'F上,∠B'RT=90°
过点S作SX⊥B'F于点X
∴E'R=![]() B'E'=1,点E'翻折后落在E'F上即为点T
B'E'=1,点E'翻折后落在E'F上即为点T
∴B'S=RT=E'R=1
∵∠SB'X=90°﹣∠RB'F=30°
∴XS=![]() B'S=
B'S=![]() ,B'X=
,B'X=![]() B'S=
B'S=![]()
∴xS=xB'+XS=﹣![]() ,yS=yB'﹣B'X=
,yS=yB'﹣B'X=![]()
∴S(﹣![]() ,
,![]() )
)
③如图5,点T在B'F上,∠B'TR=90°
∴RE'∥E'B',∠E'=∠B'E'R=60°
∴∠E'BE'=∠E'RE'=120°
∴四边形B'E'RE'是平行四边形
∵E'R=E'R
∴B'E'RE'是菱形
∴B'E'=E'R
∴△B'E'R是等边三角形
∵∠B'SR=90°,即RS⊥B'E'
∴点S为B'E'中点
∴S(﹣2,2![]() )
)
综上所述,使得以B′、R、T、S为顶点的四边形为矩形的点S坐标为(![]() ,3+
,3+![]() )或(﹣
)或(﹣![]() ,
,![]() )或(﹣2,2
)或(﹣2,2![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
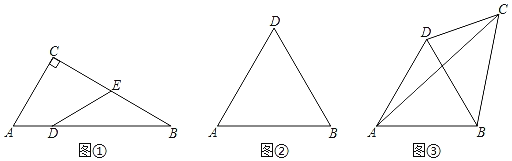
【题目】如果一个四边形的对角线把四边形分成两个三角形,一个是等边三角形,另一个是该对角线所对的角为60°的三角形,我们把这条对角线叫做这个四边形的理想对角线,这个四边形称为理想四边形.
(1)如图①,在Rt△ABC中∠C=90°,∠B=30°,AC=4,D为AB上一点,AD=2,E为BC中点,连接DE.求证:四边形ADEC为理想四边形;
(2)如图②,△ABC是等边三角形,若BD为理想对角线,四边形ABCD为理想四边形.请画图找出符合条件的C点落在怎样的图形上;
(3)在(2)的条件下,
①若△BCD为直角三角形,BC=3,求AC的长度;
②如图③,若CD=x,BC=y,AC=z,请直接写出x,y,z之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
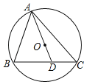
【题目】已知△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=60°,∠C=50°,则∠BAD的度数是( )
A.70°B.40°C.50°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 与点
与点![]() .
.
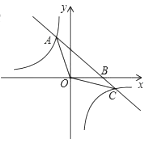
(1)求反比例函数的表达式及![]() 点坐标.
点坐标.
(2)根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.
(3)求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
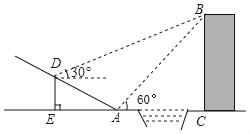
【题目】如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
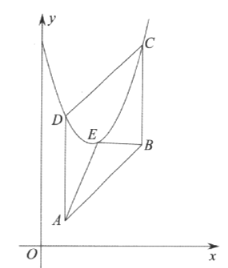
【题目】如图,在平面直角坐标系中,点![]() 是一次函数
是一次函数![]() 图象上两点,它们的横坐标分别为
图象上两点,它们的横坐标分别为![]() 其中
其中![]() ,过点
,过点![]() 分别作
分别作![]() 轴的平行线,交抛物线
轴的平行线,交抛物线![]() 于点
于点![]() ,
,![]()
(1)若![]() 求
求![]() 的值;
的值;
(2)点![]() 是抛物线上的一点,求
是抛物线上的一点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
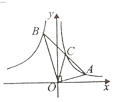
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 在反比例函数
在反比例函数![]() 的图象上,且
的图象上,且![]() ,线段
,线段![]() 交反比例函数
交反比例函数![]() 的图象于另一点
的图象于另一点![]() ,连结
,连结![]() .若点
.若点![]() 为
为![]() 的中点,
的中点,![]() ,则
,则![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.
(1)求甲、乙两种品牌的足球的单价各是多少元?
(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知第一象限的点A在反比例函数y=![]() 上,过点A作AB⊥AO交x轴于点B,∠AOB=30°,将△AOB绕点O逆时针旋转120°,点B的对应点B恰好落在反比例函数y=
上,过点A作AB⊥AO交x轴于点B,∠AOB=30°,将△AOB绕点O逆时针旋转120°,点B的对应点B恰好落在反比例函数y=![]() 上,则k的值为( )
上,则k的值为( )
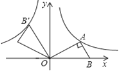
A.﹣4![]() B.﹣
B.﹣![]() C.﹣2
C.﹣2![]() D.﹣
D.﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com