练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知△ABC内接于⊙O，连接AO并延长交BC于点D，若∠B＝60°，∠C＝50°，则∠BAD的度数是（　　）

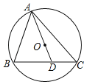
    A.70°B.40°C.50°D.60°

    【答案】B

    【解析】

    延长AD交圆O于E，连接CE，根据圆周角定理得到∠E=∠B=60°，∠ACE=90°，再由同弧所对的圆周角相等可得∠AEC=∠B=60°，再由直角三角形的性质求得∠CAE=30°，由三角形的内角和得到∠BAC=70°，最后用角的和差即可解答．

    解：延长AD交圆O于E，连接CE，

    ∴∠E=∠B=60°，∠ACE=90°，

    ∴∠CAE=90°-60°=30°，

    ∵∠B=60°，∠C=50°，

    ∴∠BAC=180°-∠B-∠ACB=70°，

    ∴∠BAD=∠BAC-∠CAE=40°，

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】居民区内的“广场舞”引起媒体关注，民勤电视台为此进行过专访报到．小平想了解本小区居民对“广场舞”的看法，进行了一次抽样调查，把居民对“广场舞”的看法分为四个层次：．非常赞同；．赞同但要有时间限制；．无所谓；．不赞同．并将调查结果绘制了图①和图②两幅不完整的统计图．请你根据图中提供的信息解答下列问题：

    （1）求本次被抽查的居民有多少人？

    （2）将图①和图②补充完整．

    （3）求图②中“”层次所在扇形的圆心角度数．

    （4）估计该小区5000名居民中对“广场舞”的看法表示赞同（包括层次和层次）的大约有多少人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如果三角形的两个内角∠α与∠β满足∠α=2∠β，那么，我们将这样的三角形称为“倍角三角形”．如果一个等腰三角形是“倍角三角形”，那么这个等腰三角形的腰长与底边长的比值为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生(七、八年级各有600名学生)的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析，过程如下：

    收集数据：

    七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77．

    八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．

    整理数据：

    七年级

    0

    1

    0

    a

    7

    1

    八年级

    1

    0

    0

    7

    b

    2

    分析数据：

    平均数

    众数

    中位数

    七年级

    78

    75

    八年级

    78

    80.5

    应用数据：

    (1)由上表填空：a= ，b= ，c= ，d= ．

    (2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人？

    (3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中（如图），已知函数的图像和反比例函数的在第一象限交于A点，其中点A的横坐标是1．

    （1）求反比例函数的解析式；

    （2）把直线平移后与轴相交于点B，且，求平移后直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为落实疫情期间的垃圾分类，树立全面环保意识，某校举行了“垃圾分类，绿色环保”知识竞赛活动，根据学生的成绩划分为，，，四个等级，并绘制了不完整的两种统计图：

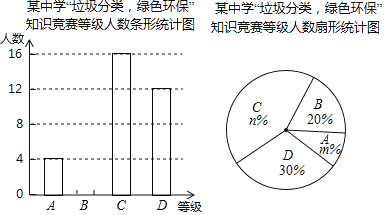
    根据图中提供的信息，回答下列问题：

    （1）参加知识竞赛的学生共有______人，并把条形统计图补充完整；

    （2）扇形统计图中，______，______，等级对应的圆心角为______度；

    （3）小明是四名获等级的学生中的一位，学校将从获等级的学生中任选取2人，参加市举办的知识竞赛，请用列表法或画树状图，求小明被选中参加区知识竞赛的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm.

    （1）若花园的面积为192m2, 求x的值；

    （2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角标系中，抛物线C：y＝与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点D为y轴正半轴上一点．且满足OD＝OC，连接BD，

    （1）如图1，点P为抛物线上位于x轴下方一点，连接PB，PD，当S△PBD最大时，连接AP，以PB为边向上作正△BPQ，连接AQ，点M与点N为直线AQ上的两点，MN＝2且点N位于M点下方，连接DN，求DN+MN+AM的最小值

    （2）如图2，在第（1）问的条件下，点C关于x轴的对称点为E，将△BOE绕着点A逆时针旋转60°得到△B′O′E′，将抛物线y＝沿着射线PA方向平移，使得平移后的抛物线C′经过点E，此时抛物线C′与x轴的右交点记为点F，连接E′F，B′F，R为线段E’F上的一点，连接B′R，将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT，在平面内找一个点S，使得以B′、R、T、S为顶点的四边形为矩形，求点S的坐标．

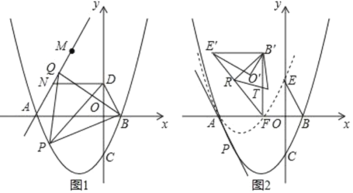
    查看答案和解析>>

    科目：初中数学 来源： 题型：

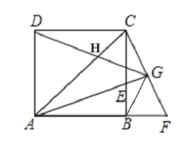
    【题目】如图，ABCD为正方形，∠CAB的角平分线交BC于点E，过点C作CF⊥AE交AE的延长线于点G，CF与AB的延长线交于点F，连接BG、DG、与AC相交于点H，则下列结论：①ABECBF；②GF=CG；③BG⊥DG；④，其中正确的是______．

    查看答案和解析>>

    同步练习册答案