
【题目】居民区内的“广场舞”引起媒体关注,民勤电视台为此进行过专访报到.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:![]() .非常赞同;
.非常赞同;![]() .赞同但要有时间限制;
.赞同但要有时间限制;![]() .无所谓;
.无所谓;![]() .不赞同.并将调查结果绘制了图①和图②两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
.不赞同.并将调查结果绘制了图①和图②两幅不完整的统计图.请你根据图中提供的信息解答下列问题:

(1)求本次被抽查的居民有多少人?
(2)将图①和图②补充完整.
(3)求图②中“![]() ”层次所在扇形的圆心角度数.
”层次所在扇形的圆心角度数.
(4)估计该小区5000名居民中对“广场舞”的看法表示赞同(包括![]() 层次和
层次和![]() 层次)的大约有多少人.
层次)的大约有多少人.
【答案】(1)本次共抽查300人;(2)补图见解析;(3)108°;(4)约有3500人.
【解析】
(1)由A层次的人数除以所占的百分比求出调查的学生总数即可;
(2)由D层次人数除以总人数求出D所占的百分比,再求出B所占的百分比,再乘以总人数可得B层次人数,用总人数乘以C层次所占的百分比可得C层次的人数,补全图形即可;
(3)用360°乘以A层次的人数所占的百分比即可得“A”层次所在扇形的圆心角的度数;
(4)求出样本中A层次与B层次的百分比之和,乘以5000即可得到结果.
解:(1)由图可知,“![]() ”层次的人有90人,占被抽查的居民的30%,
”层次的人有90人,占被抽查的居民的30%,
∴共抽查:![]() (人),
(人),
答:本次共抽查300人;
(2)“![]() ”层次:300×20%=60(人);
”层次:300×20%=60(人);
“![]() ”层次:30÷300×100%=10%;
”层次:30÷300×100%=10%;
“![]() ”层次:300-90-60-30=120(人),
”层次:300-90-60-30=120(人),
120÷300×100%=40%;
补图如下:
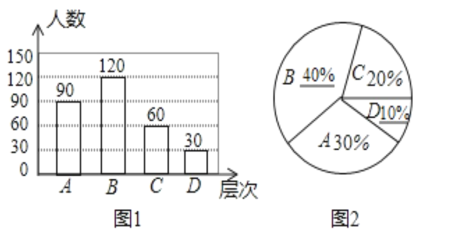 ;
;
(3)“![]() ”层次所在扇形的圆心角度数为:
”层次所在扇形的圆心角度数为:![]() ;
;
(4)![]() (人),
(人),
答:估计该小区5000名居民中对“广场舞”表示赞同的约有3500人.


科目:初中数学 来源: 题型:
【题目】体育老师统计了七年级甲、乙两个班女生的身高情况,并绘制了如下不完整的统计图.请根据图中信息,解决下列问题:
(1)求甲、乙两个班共有女生多少人?
(2)请将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角的度数.
部分所对应的扇形圆心角的度数.
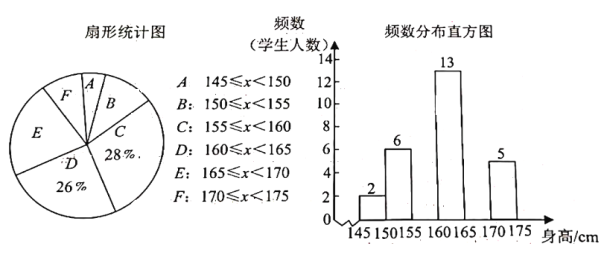
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
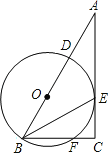
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=![]() ,D为边AC上一动点(C点除外),把线段BD绕着点D沿着顺时针的方向旋转90°至DE,连接CE,则△CDE面积的最大值为______.
,D为边AC上一动点(C点除外),把线段BD绕着点D沿着顺时针的方向旋转90°至DE,连接CE,则△CDE面积的最大值为______.
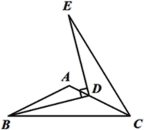
查看答案和解析>>
科目:初中数学 来源: 题型:
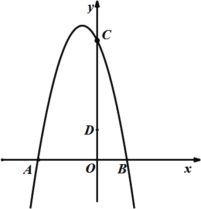
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点A、B,与
轴交于点A、B,与![]() 轴交于点C,点B的坐标为
轴交于点C,点B的坐标为![]() ,点
,点![]() 在
在![]() 轴上,连接AD.
轴上,连接AD.
(1)![]() = ;
= ;
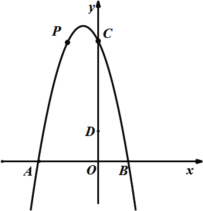
(2)若点![]() 是抛物线在第二象限上的点,过点
是抛物线在第二象限上的点,过点![]() 作PF⊥x轴,垂足为
作PF⊥x轴,垂足为![]() ,
,![]() 与
与![]() 交于点E.是否存在这样的点P,使得PE=7EF?若存在,求出点
交于点E.是否存在这样的点P,使得PE=7EF?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标大于-4,过点
的横坐标大于-4,过点![]() 作
作![]() ,垂足为H,直线
,垂足为H,直线![]() 与
与![]() 轴交于点K,且
轴交于点K,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市实验中学计划在暑假第二周的星期一至星期五开展暑假社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)乙同学随机选择两天,其中有一天是星期三的概率是多少?(列表或画树形图或列举)
查看答案和解析>>
科目:初中数学 来源: 题型:
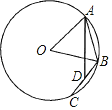
【题目】如图,已知⊙O的半径为6,点A、B在⊙O上,∠AOB=60°,动点C在⊙O上(与A、B两点不重合),连接BC,点D是BC中点,连接AD,则线段AD的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
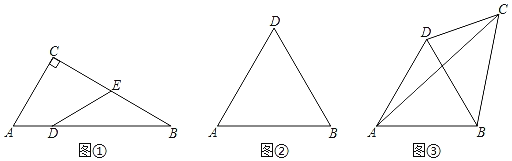
【题目】如果一个四边形的对角线把四边形分成两个三角形,一个是等边三角形,另一个是该对角线所对的角为60°的三角形,我们把这条对角线叫做这个四边形的理想对角线,这个四边形称为理想四边形.
(1)如图①,在Rt△ABC中∠C=90°,∠B=30°,AC=4,D为AB上一点,AD=2,E为BC中点,连接DE.求证:四边形ADEC为理想四边形;
(2)如图②,△ABC是等边三角形,若BD为理想对角线,四边形ABCD为理想四边形.请画图找出符合条件的C点落在怎样的图形上;
(3)在(2)的条件下,
①若△BCD为直角三角形,BC=3,求AC的长度;
②如图③,若CD=x,BC=y,AC=z,请直接写出x,y,z之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=60°,∠C=50°,则∠BAD的度数是( )
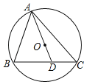
A.70°B.40°C.50°D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com