
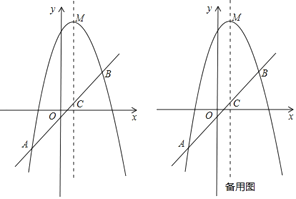
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
【答案】(1)抛物线的表达式为:![]() ,直线
,直线![]() 的表达式为:
的表达式为:![]() ;(2)存在,理由见解析;点
;(2)存在,理由见解析;点![]()
![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)二次函数表达式为:y=a(x-1)2+9,即可求解;
(2)S△DAC=2S△DCM,则![]() ,,即可求解;
,,即可求解;
(3)分AM是平行四边形的一条边、AM是平行四边形的对角线两种情况,分别求解即可.
解:(1)二次函数表达式为:![]() ,
,
将点![]() 的坐标代入上式并解得:
的坐标代入上式并解得:![]() ,
,
故抛物线的表达式为:![]() …①,
…①,
则点![]() ,
,
将点![]() 的坐标代入一次函数表达式并解得:
的坐标代入一次函数表达式并解得:
直线![]() 的表达式为:
的表达式为:![]() ;
;
(2)存在,理由:
二次函数对称轴为:![]() ,则点
,则点![]() ,
,
过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,
,
设点![]() ,点
,点![]() ,
,
∵![]() ,
,
则![]() ,
,
解得:![]() 或5(舍去5),
或5(舍去5),
故点![]() ;
;
(3)设点![]() 、点
、点![]() ,
,![]() ,
,
①当![]() 是平行四边形的一条边时,
是平行四边形的一条边时,
点![]() 向左平移4个单位向下平移16个单位得到
向左平移4个单位向下平移16个单位得到![]() ,
,
同理,点![]() 向左平移4个单位向下平移16个单位为
向左平移4个单位向下平移16个单位为![]() ,即为点
,即为点![]() ,
,
即:![]() ,
,![]() ,而
,而![]() ,
,
解得:![]() 或﹣4,
或﹣4,
故点![]() 或
或![]() ;
;
②当![]() 是平行四边形的对角线时,
是平行四边形的对角线时,
由中点公式得:![]() ,
,![]() ,而
,而![]() ,
,
解得:![]() ,
,
故点![]() 或
或![]() ;
;
综上,点![]() 或
或![]() 或
或![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
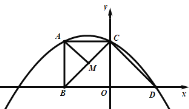
【题目】已知点![]() ,
,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 运动(
运动(![]() 不与点
不与点![]() ,
,![]() 重合),设运动时间为
重合),设运动时间为![]() 秒.
秒.
图(1) 图(2)
(1)求经过![]() ,
,![]() ,
,![]() 三点的抛物线的函数表达式;
三点的抛物线的函数表达式;
(2)点![]() 在(1)中的抛物线上,当
在(1)中的抛物线上,当![]() 为
为![]() 的中点时,若
的中点时,若![]() ,求点
,求点![]() 的坐标;
的坐标;
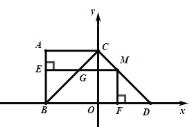
(3)当![]() 在
在![]() 上运动时,如图(2),过点
上运动时,如图(2),过点![]() 作
作![]() 轴,
轴,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,设矩形
,设矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,当
,当![]() 为何值时,
为何值时,![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
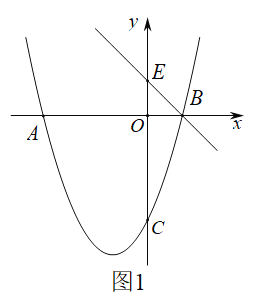
(1)求抛物线![]() 的解析式;
的解析式;
(2)如图1,点![]() 在
在![]() 轴上,连接
轴上,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
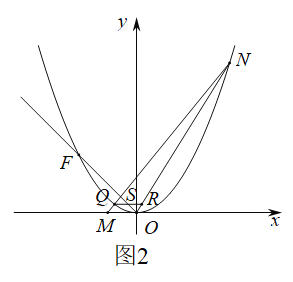
(3)如图2,将抛物线![]() 平移,使其顶点是坐标原点
平移,使其顶点是坐标原点![]() ,得到抛物线
,得到抛物线![]() ,平移直线
,平移直线![]() 经过原点
经过原点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() .点
.点![]() ,点
,点![]() 是
是![]() 第一象限内一动点,
第一象限内一动点,![]() 交
交![]() 于
于![]() 点,
点,![]() 轴分别交
轴分别交![]() 、
、![]() 于
于![]() 、
、![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,顶点P(3,-4).
(1)求抛物线的解析式;
(2)若点M在抛物线上,且△MAB的面积为24,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为(1,0),以
的坐标为(1,0),以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ,再以
,再以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ,再以
,再以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ……按此规律进行下去,则点
……按此规律进行下去,则点![]() 的坐标为_________.
的坐标为_________.
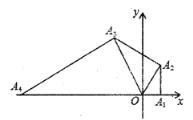
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市政府关于“垃圾不落地市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B:比较了解,C:了解较少,D:不了解”四种,并将调查结果绘制成两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生有2000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有 名;
(3)已知“非常了解”的同学有3名男生和1名女生,从中随机抽取2名进行垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
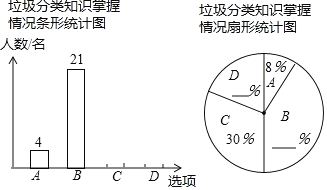
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边![]() ,以边
,以边![]() 为直径的半圆与边
为直径的半圆与边![]() ,
,![]() 分别交于点
分别交于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
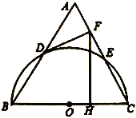
(1)判断![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)过点![]() 作
作![]() 于点
于点![]() ,若等边
,若等边![]() 的边长为8,求
的边长为8,求![]() ,
,![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用1000元购进某种水果销售,过了一段时间,又用2400元购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次贵了2元.
(1)该商店第一次购进水果多少千克?
(2)已知该水果的日销售量![]() (千克)与售价
(千克)与售价![]() (元)是一次函数关系.若售价为13元,则每天可以卖出50千克;若售价为15元,则每天可以卖出40千克.求
(元)是一次函数关系.若售价为13元,则每天可以卖出50千克;若售价为15元,则每天可以卖出40千克.求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )

A. 30![]() m B. 20
m B. 20![]() m C. 30
m C. 30![]() m D. 15
m D. 15![]() m
m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com