
����Ŀ��Ϊ��Ӧ���������ڡ�����������������������������������ijУ��������˲���ѧ������������֪ʶ���������������ѡ���Ϊ��A���dz��˽⣬B���Ƚ��˽⣬C���˽���٣�D�����˽⡱���֣��������������Ƴ�������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
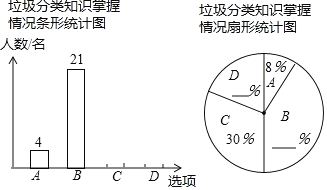
��1��������ͳ��ͼ����������
��2������Уѧ����2000�������ݵ����������Ƹ�У���dz��˽⡱�롰�Ƚ��˽⡱��ѧ������������������
��3����֪���dz��˽⡱��ͬѧ��3��������1��Ů�������������ȡ2���������������֪ʶ���������û���״ͼ���б��ķ�������ǡ�ó鵽һ��һŮ�ĸ��ʣ�
���𰸡���1���𰸼���������2��1000����3��![]() ��
��
��������
��1���ȸ���Aѡ�����������ռ����������ó��������������50,�ٸ���Bѡ����������B��ռ�ı��������Ÿ���Cѡ��ı�������ó�������������ó�Dѡ��ı������������ɣ�
��2����2000����Aѡ���Bѡ��ı��������ɹ��Ƹ�У���dz��˽��������Ƚ��˽�����ѧ������
��3�������б�����չʾ����12�ֿ��ܵĽ�����ҳ�һ��һŮ�Ľ������Ȼ����ݸ��ʵĹ�ʽ���ɵó��𰸣�
��1����������Ϊ��4��8%=50(��)��B����ռ�ٷֱ�Ϊ��21��50=42%��
C��������50��30%=15(��)��
D������Ϊ��50��4��21��15=10(��)����ռ�ٷֱ�Ϊ��10��50=20%��
��ȫͳ��ͼ��ͼ��ʾ��

��2��2000��(8%+42%)=1000(��)��
�ʴ�Ϊ��1000��
��3�����б�����ʾ���п��ܳ��ֵĽ�����£�

����12�ֿ��ܳ��ֵĽ�������С�һ��һŮ������6�֣�
��ˣ��鵽һ��һŮ�ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
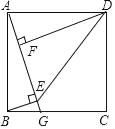
����Ŀ����ͼ��������ABCD�У�GΪBC����һ�㣬BE��AG��E��DF��AG��F������DE��
��1����֤����ABE�ա�DAF��
��2����AF=1���ı���ABED�����Ϊ6����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�������㣨1��3������3��2��������2����![]() ������������ͬʱ�ڷ���������y��
������������ͬʱ�ڷ���������y��![]() ��ͼ���ϣ�������ֱ��ΪA��B����һ���ΪC��
��ͼ���ϣ�������ֱ��ΪA��B����һ���ΪC��

��1�����������Ľ���ʽ��
��2����ֱ��AB��Ӧ��һ�κ����Ľ���ʽ��
��3������AC��BC�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ĸ�����ڼ䣬ijУ������Ա�μ���ṫ����������һ����Ըƿ����
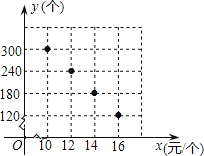
���ۣ������������������ƻ����������г����飬������Ըƿһ��ʱ���ڵ�������y(��)�����۵���x(Ԫ
/��)֮��Ķ�Ӧ��ϵ��ͼ��ʾ��
(1)���ж�y��x֮��ĺ�����ϵ�������������ϵʽ��
(2)����Ըƿ�Ľ���Ϊ6Ԫ/�������������г��������۹��ɣ�������w(Ԫ)�����۵���x(Ԫ/��)֮���
������ϵʽ��
(3)����Ըƿ�Ľ����ɱ�������900Ԫ��Ҫ����������������ʱ������Ըƿ�����۵��ۣ������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
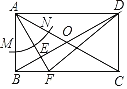
����Ŀ����ͼ���ھ���ABCD�У��Խ���AC��BD���ڵ�O����֪AB��OA�������²�����ͼ�����Ե�AΪԲ�ģ������ⳤΪ�뾶������AB��M����AC�ڵ�N���ڷֱ��Ե�M��NΪԲ�ģ��Դ���![]() MNΪ�뾶�����������ཻ�ڵ�E����������AE��BC�ڵ�F������DF����AB��
MNΪ�뾶�����������ཻ�ڵ�E����������AE��BC�ڵ�F������DF����AB��![]() �����߶�DF�ij�Ϊ_____��
�����߶�DF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �ĸ�����Ϊ����
�ĸ�����Ϊ����![]() ��ͼ���뺯��
��ͼ���뺯��![]() ��ͼ��ĺ����꣬��
��ͼ��ĺ����꣬��![]() ��ʵ��x0���ڵķ�Χ�ǣ� ��
��ʵ��x0���ڵķ�Χ�ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ�κ���y����x+b�뷴��������y��![]() ��x��0����ͼ���ڵ�A��1��3���͵�B��3��m����
��x��0����ͼ���ڵ�A��1��3���͵�B��3��m����
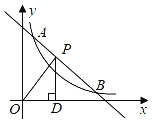
��1����գ�һ�κ����ı���ʽΪ�� ���������������ı���ʽΪ�� ����
��2����P���߶�AB��һ�㣬����P��PD��x���ڵ�D������OP������POD�����ΪS����S��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��![]() ������A��1��0���͵�B��5��0������y�ύ�ڵ�C��
������A��1��0���͵�B��5��0������y�ύ�ڵ�C��
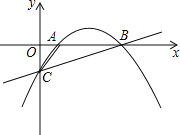
��1����������ߵĽ���ʽ��
��2���Ե�AΪԲ�ģ�����ֱ��BC���е���A������A�İ뾶��
��3����ֱ��BC�Ϸ�������������ȡһ��P������PB��PC�����ʣ���PBC������Ƿ�������ֵ�������ڣ����������ֵ�Ĵ�ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ� ��
A. �����ӣ����ڲ������Ž�Ŀ���DZ�Ȼ�¼�
B. ����һöӲ�ң�������ϵĸ���Ϊ![]() ����ʾÿ�����ξ���һ�����泯��
����ʾÿ�����ξ���һ�����泯��
C. ����һö���ȵ����������ӣ����ϵĵ�����6�ĸ���Ϊ![]() ����ʾ�����������������ӣ����׳����ϵĵ�����6����һ�¼�������Ƶ���ȶ���
����ʾ�����������������ӣ����׳����ϵĵ�����6����һ�¼�������Ƶ���ȶ���![]() ����
����
D. Ϊ�˽�ij�ֽ��ܵƵ�ʹ��������ѡ��ȫ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com