
【题目】定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 度;
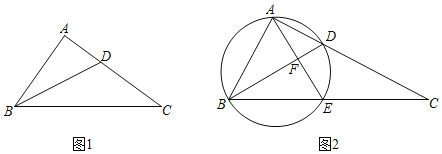
(2)如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
①求证:△BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
(3)如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连结AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.
【答案】(1)20;(2)①见解析;②存在,CE=![]() ;(3)tan∠C的值为
;(3)tan∠C的值为![]() 或
或![]() .
.
【解析】
(1)∠B不可能是α或β,当∠A=α时,∠C=β=50°,α+2β=90°,不成立;故∠A=β,∠C=α,α+2β=90°,则β=20°;
(2)①如图1,设∠=ABD∠DBC=β,∠C=α,则α+2β=90°,故△BDC是“近直角三角形”;
②∠ABE=∠C,则△ABC∽△AEB,即![]() ,即
,即![]() ,解得:AE=
,解得:AE=![]() ,即可求解.
,即可求解.
(3)①如图2所示,当∠ABD=∠DBC=β时,设BH=x,则HE=5﹣x,则AH2=AE2﹣HE2=AB2﹣HB2,即52﹣x2=62﹣(5﹣x)2,解得:x=![]() ,即可求解;
,即可求解;
②如图3所示,当∠ABD=∠C=β时,AF∶EF=AG∶GE=2∶3,则DE=2k,则AG=3k=R(圆的半径)=BG,点H是BE的中点,则GH=![]() DE=k,在△BGH中,BH=
DE=k,在△BGH中,BH=![]() =2
=2![]() k,在△ABH中,AB=5,BH=2
k,在△ABH中,AB=5,BH=2![]() k,AH=AG+HG=4k,由勾股定理得:25=8k2+16k2,解得:k=
k,AH=AG+HG=4k,由勾股定理得:25=8k2+16k2,解得:k=![]() ,即可求解.
,即可求解.
解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为20;
(2)①如图1,设∠=ABD∠DBC=β,∠C=α,
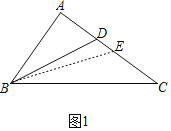
则α+2β=90°,故△BDC是“近直角三角形”;
②存在,理由:
在边AC上是否存在点E(异于点D),使得△BCE是“近直角三角形”,
AB=3,AC=4,则BC=5,
则∠ABE=∠C,则△ABC∽△AEB,
即![]() ,即
,即![]() ,解得:AE=
,解得:AE=![]() ,
,
则CE=4﹣![]() =
=![]() ;
;
(3)①如图2所示,当∠ABD=∠DBC=β时,
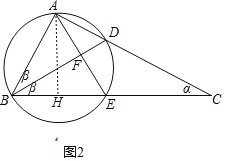
则AE⊥BF,则AF=FE=3,则AE=6,
AB=BE=5,
过点A作AH⊥BC于点H,
设BH=x,则HE=5﹣x,
则AH2=AE2﹣HE2=AB2﹣HB2,即52﹣x2=62﹣(5﹣x)2,解得:x=![]() ;
;
cos∠ABE=![]() =
=![]() =cos2β,则tan2β=
=cos2β,则tan2β=![]() ,
,
则tanα=![]() ;
;
②如图3所示,当∠ABD=∠C=β时,
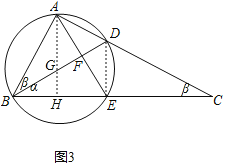
过点A作AH⊥BE交BE于点H,交BD于点G,则点G是圆的圆心(BE的中垂线与直径的交点),
∵∠AEB=∠DAE+∠C=α+β=∠ABC,故AE=AB=5,则EF=AE﹣AF=5﹣3=2,
∵DE⊥BC,AH⊥BC,
∴ED∥AH,则AF∶EF=AG∶GE=2∶3,
则DE=2k,则AG=3k=R(圆的半径)=BG,点H是BE的中点,则GH=![]() DE=k,
DE=k,
在△BGH中,BH=![]() =2
=2![]() k,
k,
在△ABH中,AB=5,BH=2![]() k,AH=AG+HG=4k,
k,AH=AG+HG=4k,
由勾股定理得:25=8k2+16k2,解得:k=![]() ;
;
在△ABD中,AB=5,BD=6k=![]() ,
,
则cos∠ABD=cosβ=![]() =
=![]() =cosC,
=cosC,
则tanC=![]() ;
;
综上,tan∠C的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论正确的是( )
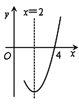
A.当x<2时,y随x增大而增大B.a-b+c<0
C.拋物线过点(-4,0)D.4a+b=0
查看答案和解析>>
科目:初中数学 来源: 题型:
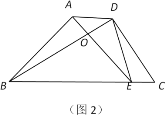
【题目】如图1,在四边形ABCD中,∠BAD=∠BDC=90°,AB=AD,∠DCB=60°,CD=8.
(1)若P是BD上一点,且PA=CD,求∠PAB的度数.
(2)①将图1中的△ABD绕点B顺时针旋转30°,点D落在边BC上的E处,AE交BD于点O,连接DE,如图2,求证:DE2=DODB;
②将图1中△ABD绕点B旋转α得到△A'BD'(A与A',D与D'是对应点),若CD'=CD,则cosα的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
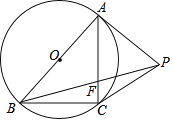
【题目】如图,PA与⊙O相切于点A,AB是⊙O的直径,在⊙O上存在一点C满足PA=PC,连结PB、AC相交于点F,且∠APB=3∠BPC,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段围成一个正方形.
的铁丝剪成两段,并把每一段围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小明该怎么剪?
,小明该怎么剪?
(2)小刚对小明说:“这两个正方形的面积之和不可能等于![]() .”小刚的说法对吗?请说明理由.
.”小刚的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地农产品专卖店收购了一种非常受欢迎的土特产,该店以![]() 元/千克收购了这种土特产
元/千克收购了这种土特产![]() 千克,若立即销往外地,每千克可以获利
千克,若立即销往外地,每千克可以获利![]() 元.根据市场调查发现,该种土特产的销售单价每天上涨
元.根据市场调查发现,该种土特产的销售单价每天上涨![]() 元/千克,为了获得更大利润,该店决定先贮藏一段时间后再出售.根据以往经验,这批土特产的贮藏时间不宜超过
元/千克,为了获得更大利润,该店决定先贮藏一段时间后再出售.根据以往经验,这批土特产的贮藏时间不宜超过![]() 天,在贮藏过程中平均每天损耗
天,在贮藏过程中平均每天损耗![]() 千克.
千克.
(1)若商家将这批土特产贮藏![]() 天后一次性出售,请完成下列表格:
天后一次性出售,请完成下列表格:
每千克土特产售价(单位:元) | 可供出售的土特产质量(单位:克) | |
现在出售 |
|
|
|
|
|
(2)将这批土特产贮藏多少天后一次性出售最终可获得总利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其它方面完全相同,若背面朝上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面朝上方在桌面上,甲从中随机抽取一张卡片,记该卡片上的数字为![]() ,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为
,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为![]() ,组成一数对
,组成一数对![]() .
.
(1)请写出![]() .所有可能出现的结果;
.所有可能出现的结果;
(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽依次卡片,卡片上述资质和为奇数则甲赢,数字之和为偶数则乙赢,你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有________(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com