
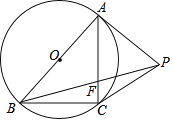
【题目】如图,PA与⊙O相切于点A,AB是⊙O的直径,在⊙O上存在一点C满足PA=PC,连结PB、AC相交于点F,且∠APB=3∠BPC,则![]() =_____.
=_____.
【答案】![]() .
.
【解析】
连接OP,OC,证明△OAP≌△OCP,可得PC与⊙O相切于点C,证明BC=CP,设OM=x,则BC=CP=AP=2x,PM=y,证得△AMP∽△OAP,可得:![]() ,证明△PMF∽△BCF,由
,证明△PMF∽△BCF,由![]() 可得出答案.
可得出答案.
解:连接OP,OC.
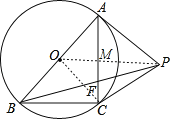
∵PA与⊙O相切于点A,PA=PC,
∴∠OAP=90°,
∵OA=OC,OP=OP,
∴△OAP≌△OCP(SSS),
∴∠OAP=∠OCP=90°,
∴PC与⊙O相切于点C,
∵∠APB=3∠BPC,∠APO=∠CPO,
∴∠CPB=∠OPB,
∵AB是⊙O的直径,
∴∠BCA=90°,
∵OP⊥AC,
∴OP∥BC,
∴∠CBP=∠CPB,
∴BC=CP=AP.
∵OA=OB,
∴OM=![]() .
.
设OM=x,则BC=CP=AP=2x,PM=y,
∵∠OAP=∠AMP=90°,∠MPA=∠APO,
∴△AMP∽△OAP,
∴![]() .
.
∴AP2=PMOP,
∴(2x)2=y(y+x),
解得:![]() ,
,![]() (舍去).
(舍去).
∵PM∥BC,
∴△PMF∽△BCF,
∴![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
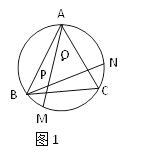

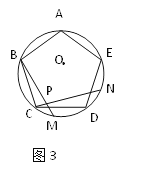
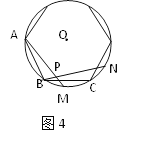
(1)求图1中∠APN的度数;
(2)图2中,∠APN的度数是_______,图3中∠APN的度数是________。
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)若由甲挑一名选手打第一场比赛,选中乙的概率是 ;
(2)任选两名同学打第一场,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b与直线y=2x+1平行,且过点(1,﹣3).
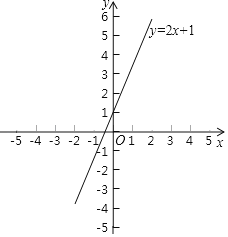
(1)求这个一次函数的关系式?
(2)画出函数图象.
(3)该函数图象与两个坐标轴围成的三角形的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
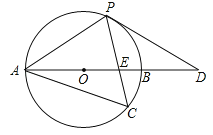
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 度;
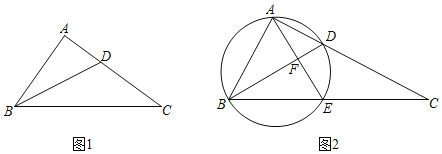
(2)如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
①求证:△BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
(3)如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连结AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的小正方形网格中,勤奋学习小组的同学画出了五边形
的小正方形网格中,勤奋学习小组的同学画出了五边形![]() 和五边形
和五边形![]() 则下列说法中,不正确的是( )
则下列说法中,不正确的是( )

A.五边形![]()
![]() 五边形
五边形![]()
B.![]()
C.五边形![]() 的周长是五边形
的周长是五边形![]() 周长的
周长的![]() 倍.
倍.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
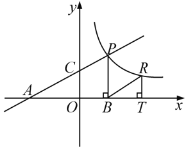
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥![]() 轴于B,且S△ABP=9.
轴于B,且S△ABP=9.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥![]() 轴于T,当△BRT与△AOC相似时,求点R的坐标.
轴于T,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉厂生产某品牌的面粉按质量分5个档次,生产第一档(最低档次)面粉,每天能生产55吨,每吨利润1000元.生产面粉的质量每提高一个档次,每吨利润会增加200元,但每天的产量会减少5吨.
(1)若生产第![]() 档次的面粉每天的总利润为
档次的面粉每天的总利润为![]() 元(其中
元(其中![]() 为正整数,且
为正整数,且![]() ),求生产哪个档次的面粉时,每天的利润最大,每天的最大利润是多少元?
),求生产哪个档次的面粉时,每天的利润最大,每天的最大利润是多少元?
(2)若生产第![]() 档次的面粉一天的总利润为60000元,求该面粉的质量档次.
档次的面粉一天的总利润为60000元,求该面粉的质量档次.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com