
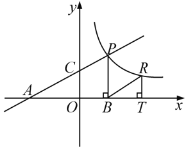
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥![]() 轴于B,且S△ABP=9.
轴于B,且S△ABP=9.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥![]() 轴于T,当△BRT与△AOC相似时,求点R的坐标.
轴于T,当△BRT与△AOC相似时,求点R的坐标.
【答案】(1)详见解析;(2)P为(2,3);(3)R(![]() )或(3,0)
)或(3,0)
【解析】
(1)由一对公共角相等,一对直角相等,利用两对角相等的三角形相似即可得证;
(2)先求出点A、C的坐标,设出A(x,0),C(0,y)代入直线的解析式可知;由△AOC∽△ABP,利用线段比求出BP,AB的值从而可求出点P的坐标即可;
(3)把P坐标代入求出反比例函数,设R点坐标为(![]() ),根据△BRT与△AOC相似分两种情况,利用线段比建立方程,求出a的值,即可确定出R坐标.
),根据△BRT与△AOC相似分两种情况,利用线段比建立方程,求出a的值,即可确定出R坐标.
解:(1)∵∠CAO=∠PAB,∠AOC=∠ABP=90°,
∴△AOC∽△ABP;
(2)设A(x,0),C(0,y)由题意得:
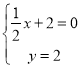 ,解得:
,解得:![]() ,
,
∴A(-4,0),C(0,2),即AO=4,OC=2,
又∵S△ABP=9,
∴ABBP=18,
又∵PB⊥x轴,
∴OC∥PB,
∴△AOC∽△ABP,
∴![]() ,即
,即![]() ,
,
∴2BP=AB,
∴2BP2=18,
∴BP2=9,
∴BP=3,
∴AB=6,
∴P点坐标为(2,3);
(3)设反比例函数为![]() ,则
,则![]() ,即
,即![]() ,
,
可设R点为(![]() ),则RT=
),则RT=![]() ,TB=
,TB=![]()
①要△BRT∽△ACO,则只要![]() ,
,
∴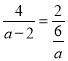 ,解得:
,解得:![]() ,
,
∴![]() ;
;
∴点R的坐标为:(![]() ,
,![]() );
);
②若△BRT∽△CAO,则只要![]() ,
,
∴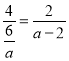 ,解得:
,解得:![]() ,
,
∴![]() ,
,
∴点R的坐标为:(3,2);
综合上述可知,点R为:(![]() )或(3,2).
)或(3,2).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】给出如下定义:对于⊙O的弦MN和⊙O外一点P(M,O,N三点不共线,且点P,O在直线MN的异侧),当∠MPN+∠MON=180°时,则称点P是线段MN关于点O的关联点.图1是点P为线段MN关于点O的关联点的示意图.

在平面直角坐标系xOy中,⊙O的半径为1.
(1)如图2,已知M(![]() ,
,![]() ),N(
),N(![]() ,﹣
,﹣![]() ),在A(1,0),B(1,1),C(
),在A(1,0),B(1,1),C(![]() ,0)三点中,是线段MN关于点O的关联点的是 ;
,0)三点中,是线段MN关于点O的关联点的是 ;
(2)如图3,M(0,1),N(![]() ,﹣
,﹣![]() ),点D是线段MN关于点O的关联点.
),点D是线段MN关于点O的关联点.
①∠MDN的大小为 ;
②在第一象限内有一点E(![]() m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
③点F在直线y=﹣![]() x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
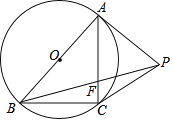
【题目】如图,PA与⊙O相切于点A,AB是⊙O的直径,在⊙O上存在一点C满足PA=PC,连结PB、AC相交于点F,且∠APB=3∠BPC,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地农产品专卖店收购了一种非常受欢迎的土特产,该店以![]() 元/千克收购了这种土特产
元/千克收购了这种土特产![]() 千克,若立即销往外地,每千克可以获利
千克,若立即销往外地,每千克可以获利![]() 元.根据市场调查发现,该种土特产的销售单价每天上涨
元.根据市场调查发现,该种土特产的销售单价每天上涨![]() 元/千克,为了获得更大利润,该店决定先贮藏一段时间后再出售.根据以往经验,这批土特产的贮藏时间不宜超过
元/千克,为了获得更大利润,该店决定先贮藏一段时间后再出售.根据以往经验,这批土特产的贮藏时间不宜超过![]() 天,在贮藏过程中平均每天损耗
天,在贮藏过程中平均每天损耗![]() 千克.
千克.
(1)若商家将这批土特产贮藏![]() 天后一次性出售,请完成下列表格:
天后一次性出售,请完成下列表格:
每千克土特产售价(单位:元) | 可供出售的土特产质量(单位:克) | |
现在出售 |
|
|
|
|
|
(2)将这批土特产贮藏多少天后一次性出售最终可获得总利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
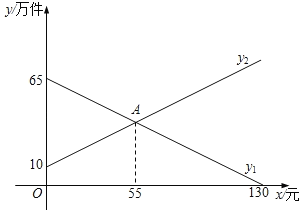
【题目】某商品的市场销售量y1(万件)和生产量y2(万件)都是该商品的定价x(元/件)的一次函数,其函数图象如图所示.
(1)分别求出y1、y2与x之间的函数表达式;
(2)若生产一件该商品成本为10元,未售出的商品一律报废.
①请解释点A的实际意义,并求出此时所获得的利润;
②该商品的定价为多少元时获得的利润最大,最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其它方面完全相同,若背面朝上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面朝上方在桌面上,甲从中随机抽取一张卡片,记该卡片上的数字为![]() ,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为
,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为![]() ,组成一数对
,组成一数对![]() .
.
(1)请写出![]() .所有可能出现的结果;
.所有可能出现的结果;
(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽依次卡片,卡片上述资质和为奇数则甲赢,数字之和为偶数则乙赢,你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做“用频率估计概率”的试验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )
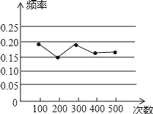
A. 任意买一张电影票,座位号是2的倍数的概率
B. 一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C. 抛一个质地均匀的正方体骰子,落下后朝上的面点数是3
D. 一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+2mx+m﹣4=0;
(1)若该方程没有实数根,求m的取值范围.
(2)怎样平移函数y=mx2+2mx+m﹣4的图象,可以得到函数y=mx2的图象?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com