
【题目】(1)如图,DE∥BC,∠1 = ∠3 ,请说明 FG ∥ DC ;
(2)若把题设中 DE ∥ BC 与结论中 FG ∥ DC 对调,命题还成立吗?试证明。
(3)若把题设中∠1=∠3 与结论中 FG ∥ DC 对调呢?试证明。

【答案】(1)见解析;(2)成立;(3)成立
【解析】
(1)求出CD∥FG,根据平行线的性质得出∠2=∠3,求出∠1=∠2,根据平行线的判定得出即可;
(2)根据平行线的性质推出∠1=∠2,求出∠2=∠3,根据平行线的判定得出CD∥FG,根据平行线的性质得出即可;
(3)求出CD∥FG,根据平行线的性质得出∠2=∠3,∠1=∠2,即可得出答案.
解:(1)因为DE∥BC,
所以∠1=∠2.
又∠1=∠3,
所以∠2=∠3,
所以FG∥DC.
(2)命题还成立.
理由:因为FG∥DC,所以∠2=∠3.
因为∠1=∠3,所以∠2=∠1,
所以DE∥BC.
(3)命题还成立.
理由:因为DE∥BC,
所以∠1=∠2.
又因为FG∥DC,
所以∠2=∠3,所以∠l=∠3.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.
(1)用关于x的代数式表示PA+PD;
(2)求出PA+PD的最小值;
(3)仿(2)的做法,构造图形,求![]() 的最小值;
的最小值;
(4)直接写出![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要900元;若购进甲种花卉40盆,乙种花卉30盆,需要960元.
(1)求购进甲、乙两种花卉每盆各需多少元?
(2)该花店购进甲,乙两种花卉共100盆,甲种花卉每盆售价20元,乙种花齐每盆售价16元,现该花店把100盆花卉全部售出,若获利超过480元,则至少购进甲种花卉多少盆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°﹣∠ABD;
④BD平分∠ADC;
⑤∠BDC=![]() ∠BAC.
∠BAC.
其中正确的结论有( )

A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
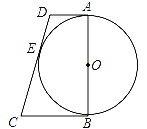
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.

(1)若∣x+2y-5∣+∣2x-y∣=0,试分别求出1秒钟后,A、B两点的坐标.
(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.

(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?
请写出你的结论并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平等于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后第2015次相遇地点的坐标是( )
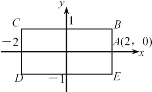
A. (2,0)B. (-1,-1)C. (-2,1)D. (-1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=![]() ,则AD=______ .
,则AD=______ .
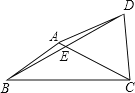
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
![]()
A. P B. R C. Q D. T
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com