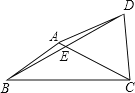
【题目】如图，在四边形ABCD中，对角线AC、BD交于点E，点E为BD的中点，∠BAC+∠BDC=180°，AB=CD=5，tan∠ACB=
，则AD=______ ．
【答案】2
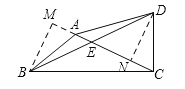
【解析】解：过B作BM⊥CA，交CA的延长线于M，过D作DN⊥CA，垂足为N，∴∠BME=∠DNC=90°．∵点E为BD的中点，∴BE=DE．∵∠BEM=∠DEN，∴△BME≌△DNE，∴BM=DN．∵AB=CD，∴Rt△ABM≌Rt△DCN，∴∠BAM=∠DCN．∵∠BAC+∠BDC=180°，∠BAC+∠BAM=180°，∴∠BDC=∠BAM，∴∠BDC=∠DCN，∴DE=CE，∴BE=CE=DE，∴∠DBC=∠ECB，∴∠DBC+∠BDC=∠ECB+∠DCN，∴△BCD是直角三角形．∵tan∠ACB=
，∴tan∠DBC=．∵DC=5，∴BC=10，在△BMC中，设BM=x，则CM=2x，由勾股定理得：x2+（2x）2=102，x=±
，∴BM=DN=，CM=
，由勾股定理得：AM=
=
=
，∴CN=AM=，∴AN=CM﹣AM﹣CN=﹣﹣=，在△ADN中，AD=
=
=
=
．故答案为：．
科目：初中数学 来源： 题型：
【题目】规定：满足（1）各边互不相等且均为整数；（2）最短边上的高与最长边上的高的比值为整数k。这样的三角形称为比高三角形，其中k叫做比高系数。根据规定解答下列问题：
（1）周长为13的比高三角形的比高系数k= ；
（2）比高三角形△ABC三边与它的比高系数k之间满足BC-AC=AC-AB=k2，求△ABC的周长的最小值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图，DE∥BC,∠1 = ∠3 ，请说明 FG ∥ DC ；
（2）若把题设中 DE ∥ BC 与结论中 FG ∥ DC 对调，命题还成立吗？试证明。
（3）若把题设中∠1＝∠3 与结论中 FG ∥ DC 对调呢？试证明。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】打折前，买6件A商品和3件B商品用了108元，买5件A商品和1件B商品用了84元，打折后买5件A商品和5件B商品用了80元。问打折后买5件A商品和5件B商品比不打折少花多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
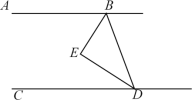
【题目】如图，AB∥CD，BE平分∠ABD，DE平分∠BDC。
（1）求证：BE⊥DE；
（2）H是直线CD上一动点（不与D重合），HI平分∠HBD交CD于点I。请你画出图形，并猜想∠EBI与∠BHD的数量关系，且说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c.
(1)已知c＝8
，∠A＝60°，求∠B，a，b；
(2)已知a＝3
，∠A＝45°，求∠B，b，c.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）计算：（-8xy2）（-
x）3+（-2x4）4+2x10（-2x2）3
（2）先化简，再求值：（y+2）（y2-2y+1）-y（y2+1），其中y=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．
性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．
理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．
应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．
（1）求证：△AOB和△AOE是“友好三角形”；
（2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．
探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的
，请直接写出△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
