
【题目】规定:满足(1)各边互不相等且均为整数;(2)最短边上的高与最长边上的高的比值为整数k。这样的三角形称为比高三角形,其中k叫做比高系数。根据规定解答下列问题:
(1)周长为13的比高三角形的比高系数k= ;
(2)比高三角形△ABC三边与它的比高系数k之间满足BC-AC=AC-AB=k2,求△ABC的周长的最小值。
【答案】(1)k=3或2;(2)△ABC的周长的最小值36
【解析】
(1)由三角形面积可知最短边上的高与最长边上的高的比值等于最长边与最短边的比值为整数k,因此根据三角形的周长确定出其三边长,求其最长边与最短边的比值即可;
(2)由题意可知当K=2时△ABC的周长有最小值,可设AB为 x ,AC为y,BC=2x,根据BC-AC=AC-AB=k2,列出关于x,y的二元一次方程组,求解即可.
(1)由三角形面积可知最短边上的高与最长边上的高的比值等于最长边与最短边的比值为整数k,周长为13,各边互不相等且均为整数的三角形只有三个分别为 2,5,6或3,4,6,所以k=3或2
(2)∵各边互不相等且均为整数
∴k≥2
∴k2 ≥4
∴当k=2时△ABC的周长有最小值。
设AB为 x ,AC为y,BC=2x
列方程组得![]()
解得方程组得![]()
![]() 2x=16
2x=16
∴△ABC的周长的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.
(1)用关于x的代数式表示PA+PD;
(2)求出PA+PD的最小值;
(3)仿(2)的做法,构造图形,求![]() 的最小值;
的最小值;
(4)直接写出![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=![]() (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )

A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要900元;若购进甲种花卉40盆,乙种花卉30盆,需要960元.
(1)求购进甲、乙两种花卉每盆各需多少元?
(2)该花店购进甲,乙两种花卉共100盆,甲种花卉每盆售价20元,乙种花齐每盆售价16元,现该花店把100盆花卉全部售出,若获利超过480元,则至少购进甲种花卉多少盆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°﹣∠ABD;
④BD平分∠ADC;
⑤∠BDC=![]() ∠BAC.
∠BAC.
其中正确的结论有( )

A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
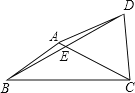
【题目】如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=![]() ,则AD=______ .
,则AD=______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com