【题目】解方程：（1）
；（2）
；（3）
【答案】（1）x＝
；（2）x＝
；（3）x＝4．
【解析】
（1）根据一元一次方程的解法，移项，合并同类项，系数化为1即可得解；
（2）根据一元一次方程的解法，去括号，移项，合并同类项，系数化为1即可得解；
（3）是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．
（1）移项，得3x＝8-15，
合并同类项，得3x＝-7，
系数化为1得，x＝；
（2）去括号，得，7x-4x+6＝10，
移项，得，7x-4x＝10-6，
合并同类项，得3x＝4，
系数化为1，得x＝；
（3）去分母，得3（x＋2）2（2x-1）＝12，
去括号，得3x＋64x+2＝12，
移项得，3x4x＝122-6，
合并同类项得，x＝4，
系数化为1得，x＝4．
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案科目：初中数学 来源： 题型：
【题目】如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：
①AD∥BC；
②∠ACB=2∠ADB；
③∠ADC=90°﹣∠ABD；
④BD平分∠ADC；
⑤∠BDC=
∠BAC．
其中正确的结论有（ ）
A．2个 B．3个 C．4个 D．5个
查看答案和解析>>
科目：初中数学 来源： 题型：
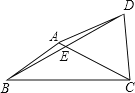
【题目】如图，在四边形ABCD中，对角线AC、BD交于点E，点E为BD的中点，∠BAC+∠BDC=180°，AB=CD=5，tan∠ACB=
，则AD=______ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD=2∠ACB．若DG=3，EC=1，则DE的长为（ ）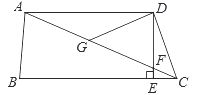
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，点
坐标为
，点
坐标为
，过点
作直线
轴，垂足为
，交线段
于点
.
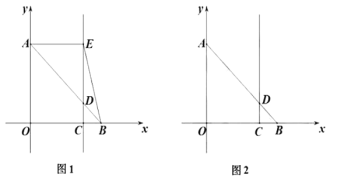
（1）如图1，过点作
，垂足为
，连接
.
①填空：
的面积为______；②点
为直线
上一动点，当
时，求点的坐标；
（2）如图2，点
为线段延长线上一点，连接
，
，线段交于点
，若
，请直接写出点的坐标为______.
查看答案和解析>>
科目：初中数学 来源： 题型：
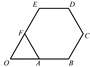
【题目】如图，正六边形ABCDEF的边长为
，延长BA，EF交于点O.以O为原点，以边AB所在的直线为
轴建立平面直角坐标系，则直线DF与直线AE的交点坐标是(_______).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数轴的单位长度为1，如果P，Q表示的数互为相反数，那么图中的4个点中，哪一个点表示的数的平方值最大（ ）
A. P B. R C. Q D. T
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】4件同型号的产品中，有1件不合格品和3件合格品．
（1）从这4件产品中随机抽取1件进行检测，求抽到的是不合格品的概率；
（2）从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；
（3）在这4件产品中加入x件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出x的值大约是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于气温，有的地方用摄氏度表示，有的地方用华氏温度表示，从温度计上可以看出，摄氏温度
与华氏温度
有如下对应的关系．下列说法不正确的是( )
A. 摄氏温度与华氏温度都是变量，摄氏温度
是自变量，华氏温度
是因变量
B. 随着摄氏温度
的逐渐升高，华氏温度
也逐新升高
C. 摄氏温度每升高
，华氏温度升高
D. 当摄氏温度为
时，华氏温度为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com