
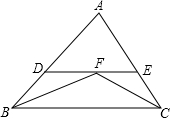
 如图所示,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC交AB于D,交AC于E.若AB=9cm,AC=8cm,则△ADE的周长是多少?
如图所示,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC交AB于D,交AC于E.若AB=9cm,AC=8cm,则△ADE的周长是多少?  培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+a)(a+1) | B. | ($\frac{1}{2}$x+y)(-y+$\frac{1}{2}$x) | C. | (x2-y)(x+y2) | D. | (x-y)(-x+y) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线互相平分的四边形是平行四边形 | |
| D. | 对角线平分每一组对角的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
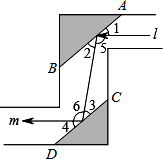 如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?
如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com