
【题目】某校九年级共有400名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,将下面的过程补全.
收集数据:
调查小组选取40名学生的体质健康测试成绩作为样本,数据如下:
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
整理、描述数据:
2018年九年级部分学生学生的体质健康测试成绩统计表
成绩 | 50≤x<55 | 55≤x<60 | 60≤x<65 | 65≤x<70 | 70≤x<75 |
人数 | 1 | 1 | 2 | 2 | 4 |
成绩 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x<100 |
人数 | 5 | a | b | 5 | 2 |
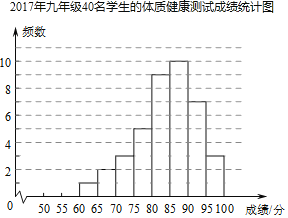
分析数据:
(1)写出表中的a、b的值;
(2)分析上面的统计图、表,你认为学生的体重健康测试成绩是2017年还是2018年的好?说明你的理由.(至少写出两条).
(3)体育老师根据2018年的统计数据,安排80分以下的学生进行体育锻炼,那么全年级大约有多少人参加?
【答案】(1)a=8,b=10;(2)去年的体质健康测试成绩比今年好,理由见解析;(3)全年级约有150名同学参加此项目.
【解析】
(1)整理、描述数据:根据所给数据计数即可得;
(2)分析数据、得出结论:将2017、2018两年的数据比较即可得(合理即可),(3)用总人数乘以2018年80分以下的同学数占被调查人数的比例可得.
(1)调查40人中体质健康测试成绩在80≤x<85之间的有8人,85≤x<90之间的有10人,
故答案为:a=8,b=10,
(2)去年的体质健康测试成绩比今年好,理由:去年较今年低分更少,高分更多,平均分更大.
(3)![]() (人),
(人),
答:全年级约有150名同学参加此项目.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
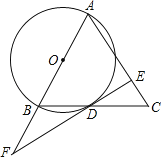
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.
(1)求证:DE⊥AC;
(2)若AB=10,BF=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
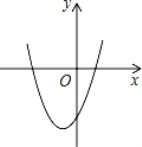
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“作已知角的角平分线”的尺规作图过程.
已知:如图,∠AOB.
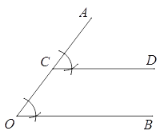
求作:∠AOB的角平分线OP.
作法:如图,
①在射线OA上任取点C;
②作∠ACD=∠AOB;
③以点C为圆心CO长为半径画圆,交射线CD于点P;
④作射线OP;
所以射线OP即为所求.
根据小元设计的尺规作图过程,完成以下任务.
(1)补全图形;
(2)完成下面的证明:
证明:∵ ∠ACD=∠AOB,
∴ CD∥OB(____________)(填推理的依据).
∴∠BOP=∠CPO.
又∵ OC=CP,
∴∠COP=∠CPO(____________)(填推理的依据).
∴∠COP=∠BOP.
∴ OP平分∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )
![]()
A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知![]() ≈1.732,tan20°≈0.36,结果精确到0.1)
≈1.732,tan20°≈0.36,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
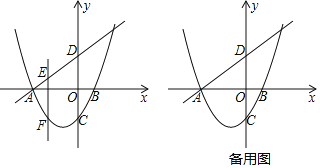
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由;
(3)在平面直角坐标系内存在点G,使得G,E,D,C为顶点的四边形为菱形,请直接写出点G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com