
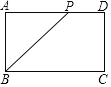
【题目】如图:在矩形ABCD中,AB=1.BC=![]() ,P为边AD上任意一点,连接PB,则PB+
,P为边AD上任意一点,连接PB,则PB+![]() PD的最小值为( )
PD的最小值为( )
A.![]() B.2C.
B.2C.![]() D.
D.![]()
【答案】C
【解析】
连接BD,根据矩形ABCD中,AB=DC=1.BC=![]() ,可得tan∠DBC=
,可得tan∠DBC=![]() ,得∠DBC=30°,作∠DBN=∠DBC=30°,过点D作DM⊥BN于点M,BN交AD于点P,此时BP+
,得∠DBC=30°,作∠DBN=∠DBC=30°,过点D作DM⊥BN于点M,BN交AD于点P,此时BP+![]() PD=BP+PM最小,最小值为BM的长.
PD=BP+PM最小,最小值为BM的长.
连接BD,
在矩形ABCD中,AB=DC=1,BC=![]() ,
,
∴tan∠DBC=![]() =
=![]() ,
,
∴∠DBC=30°
作∠DBN=∠DBC=30°,
过点D作DM⊥BN于点M,BN交AD于点P.
∴∠MDB=60°,
∵AD∥BC
∴∠PDB=∠DBC=30°,
∴∠MDP=30°,
∴PM=![]() PD,
PD,
此时,BP+![]() PD的最小值=BP+PM=BM,
PD的最小值=BP+PM=BM,
∵∠MBD=∠CBD,∠BMD=∠C=90°,BD=BD
∴△BMD≌△BCD(AAS),
∴BM=BC=![]() ,
,
答:PB+![]() PD的最小值为
PD的最小值为![]() .
.
故选:C.



 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )

A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工人打算用不锈钢条加工一个面积为0.8平方米的矩形模具.假设模具的长与宽分别为x米和y米.
(1)你能写出y与x之间的函数解析式吗?
(2)变量y与x是什么函数关系?
(3)已知这种不锈钢条每米6元,若想使模具的长比宽多1.6米,则加工这个模具共需花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴、y轴相交于P、Q两点,与
与x轴、y轴相交于P、Q两点,与![]() 的图象相交于
的图象相交于![]() 两点,连接OA,OB,给出下列结论:①
两点,连接OA,OB,给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④不等式
;④不等式![]() 的解集是
的解集是![]() 或
或![]() ,其中正确的是( )
,其中正确的是( )
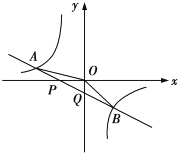
A.②③B.③④C.①②③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
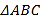
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是住宅区内的两幢楼,它们的高![]() ,两楼间的距离
,两楼间的距离![]() ,现需了解甲楼对乙楼的采光的影响情况.
,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为![]() 角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);
角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com