
若不等式组
 有实数解,则实数m的取值范围是( )
有实数解,则实数m的取值范围是( )
A.m≤
 B.m<
B.m<
 C.m>
C.m>
 D.m≥
D.m≥

科目:初中数学 来源: 题型:
如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
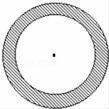
如图是在地上画出的半径分别为2m和3m的同心圆.现在你和另一人分别蒙上眼睛,并在一定距离外向圈内掷一粒较小的石子,规定一人掷中小圆内得胜,另一人掷中阴影部分得胜,未掷入半径为3m的圆内或石子压在圆周上都不算.
(1)你会选择掷中小圆内得胜,还是掷中阴影部分得胜?为什么?
(2)你认为这个游戏公平吗?如果不公平,那么大圆不变,小圆半径是多少时,使得仍按原规则进行,游戏是公平的?(只需写出小圆半径,不必说明原因)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
 ,
,
 )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
在直角坐标系中,一条直线经过A(﹣1,5),P(﹣2,a),B(3,﹣3)三点.
(1)求a的值;
(2)设这条直线与y轴相交于点D,求△OPD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
 市和
市和 市分别有库存的某联合收割机12台和6台,现决定开往
市分别有库存的某联合收割机12台和6台,现决定开往 市10台和
市10台和 市8台,已知从
市8台,已知从 市开往
市开往 市、
市、 市的油料费分别为每台400元和800元,从
市的油料费分别为每台400元和800元,从 市开往
市开往 市和
市和 市的油料费分别为每台300元和500元.
市的油料费分别为每台300元和500元.
(1)设 市运往
市运往 市的联合收割机为
市的联合收割机为 台,求运费
台,求运费 关于
关于 的函数关系式.
的函数关系式.
(2)若总运费不超过9000元,问有几种调运方案?
(3)求出总运费最低的调运方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
若|m|=2,|n|=3,则点A(m,n)( )
A.四个象限均有可能
B.在第一象限或第三象限或第四象限
C.在第一象限或第二象限
D.在第二象限或第三象限或第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com