
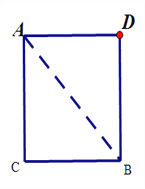
����Ŀ��С���ְֽ�ľ��ʦ������һ�ȸ�Ϊ2 m����Ϊ1��5 m����ABCD����ʦ����װ����֮�����ܾ����Ű�װ�ò����������ݾ���һ���Ű�װ���Ƿ������Ҫȡ���ڡ�ACB������ACB��ֱ�Ǿͱ���������ֻ��һ�ѹ����ľ��ߣ���������ѧ֪ʶȥ����С���ְ���֤�������Ƿ�װ�ı�.
������ѧ֪ʶ��֪�����������߶� �ij��ȣ�
�������������߶γ���Ϊ2.5 m������������ѧ֪ʶ��
С���ְ��ж��Ű�װ���Ƿ����
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ(4x2��mx��3y��4)��(8nx2��x��2y��3)��ֵ����ĸx��ȡֵ�أ������ʽ(��m2��2mn��n2)��2(mn��3m2)��3(2n2��mn)��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������O��ֱ��EF��BD���ҽ�AC�ڵ�E����BC�ڵ�F������BE��DF����BEƽ�֡�ABD.
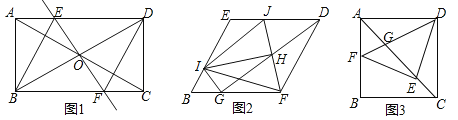
��1������֤���ı���BFDE�����Σ������EBF�Ķ�����
��2���ѣ�1��������BFDE���з����о�����ͼ2��G��I�ֱ���BF��BE���ϣ���BG=BI������GD��HΪGD���е㣬����FH�����ӳ�FH��ED�ڵ�J������IJ��IH��IF��IG����̽���߶�IH��FH֮�������������ϵ����˵�����ɣ�
��3���ѣ�1���о���ABCD�������⻯̽������ͼ3������ABCD����AB=ADʱ����E�ǶԽ���AC��һ�㣬����DE����EF��DE������Ϊ��E����AB�ڵ�F������DF����AC�ڵ�G����ֱ��д���߶�AG��GE��EC����֮�������������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8��ײˣ���ÿ��25ǧ��Ϊ����������ǧ�������������������ǧ���������������ƺ�
�ļ�¼���£��ش��������⣺

��1����8��ײ�����ӽ������������ײ��� ǧ�ˣ�
��2���������ײ���2Ԫ �M ǧ�˵ļ۸���ۣ��������ײ�һ���ɻ�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
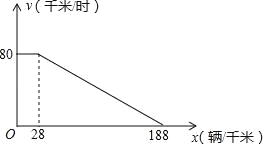
����Ŀ�������з�չ ��ͨ���������ɶ��н��������ij��������˻��±����Ķ���·���ſ���ͨ�����蹤�̣����ɺ����������·��ͨ���������о�������ij������£������ϵij����ٶ�V����λ��ǧ��/ʱ���dz����ܶ�x����λ����/ǧ�ף��ĺ������ҵ�0��x��28ʱ��V=80����28��x��188ʱ��V��x��һ�κ�����������ϵ��ͼ��ʾ��
��1����28��x��188ʱ��V����x�ĺ�������ʽ��
��2���������ٶ�V������50ǧ��/ʱ�������ܶ�xΪ����ʱ��������P����λ����/ʱ���ﵽ��������һ���ֵ��
��ע���������ǵ�λʱ����ͨ���۲��ij����������㹫ʽΪ��������=�����ٶ��������ܶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
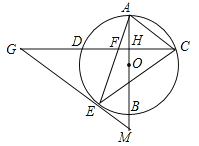
����Ŀ����ͼ��AB����O��ֱ������CD��AB������ΪH������AC����![]() ��һ��E��EG��AC��CD���ӳ����ڵ�G������AE��CD�ڵ�F����EG=FG������CE��
��һ��E��EG��AC��CD���ӳ����ڵ�G������AE��CD�ڵ�F����EG=FG������CE��
��1����֤����ECF�ס�GCE��
��2����֤��EG����O�����ߣ�
��3���ӳ�AB��GE���ӳ����ڵ�M����tanG=![]() ��AH=
��AH=![]() ����EM��ֵ��
����EM��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ӼҲ��е�������վ̨���ȹ�����ȥѧУ. ͼ�е����߱�ʾС�����г�s(km)������ʱ��t(min)֮��ĺ�����ϵ. ����˵���������

A. �����8km������30min B. ���ȹ�����ʱ��Ϊ6min
C. �����е��ٶ���100m/min D. ���������ٶ���350m/min
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2��2x+c��a��0����x�ᡢy��ֱ��ڵ�A��B��C���㣬��֪��A����2��0������C��0����8������D�������ߵĶ��㣮
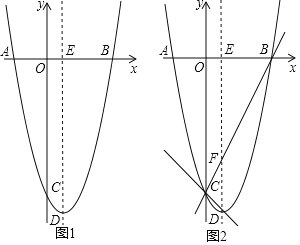
��1���������ߵĽ���ʽ������D�����ꣻ
��2����ͼ1�������ߵĶԳ�����x�ύ�ڵ�E��������������������һ��P������EBP��ֱ��EP�۵���ʹ��B�Ķ�Ӧ��B'���������ߵĶԳ����ϣ����P�����ꣻ
��3����ͼ2����BC�������ߵĶԳ����ڵ�F����ֱ��CD����M��ֱ��CD�ϵĶ��㣬��N��ƽ����һ�㣬���Ե�B��F��M��NΪ������ı���������ʱ����ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
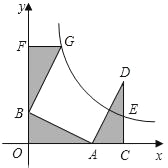
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B�ֱ���x��y���ϣ���D�ڵ�һ�����ڣ�DC��x���ڵ�C��AO=CD=2��AB=DA=![]() ������������y=
������������y=![]() ��k��0����ͼ���CD���е�E��
��k��0����ͼ���CD���е�E��
��1����k��ֵ��
��2����BFG�͡�DCA����ij������ĶԳƣ����е�F��y���ϣ����жϵ�G�Ƿ��ڷ�����������ͼ���ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com