

分析 模型建立:根据折叠的性质即可得出BC=BE,BE=AE,代换即可得出结论;
模型应用:(1)先根据模型建立中的结论依次求出OB,OE,最后用勾股定理即可求出BE,即可得出结论.
(2)求是否会受到台风的影响,其实就是求A到BC的距离是否大于台风影响范围的半径,如果大于,则不受影响,反之则受影响.如果过A作AD⊥BC于D,AD就是所求的线段.直角三角形ABD中,有∠ABD的度数,有AB的长,AD就不难求出了.然后根据题目给出的条件判断出时几级风.
解答 解:模型建立:BC与AB的关系为AB=2BC,
【】里面是折叠出∠A=30°的理由,
【由折叠得,∠CBD=∠ABD=∠A,
∵∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠CBD+∠ABD+∠A=90°,
∴∠A=30°,】
理由:由折叠得,BC=BE,BE=AE,
∴AB=AE+BE=2BE=2BC,
模型应用:(1)如图2,根据模型建立的结论,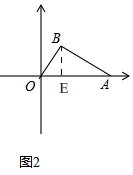 在Rt△OAB中,∠OAB=30°,OA=4,
在Rt△OAB中,∠OAB=30°,OA=4,
∴∠AOB=90°-∠OAB=60°,OB=$\frac{1}{2}$OA=2,
过点B作BE⊥OA于E,
∴∠AEB=90°,
∴∠OBE=90°-∠AOB=30°,
∴OE=$\frac{1}{2}$OB=1,
在Rt△OBE中,根据勾股定理得,BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=$\sqrt{3}$,
∴B(1,$\sqrt{3}$);
(2)该城市会受到这次台风的影响.
理由是:如图3,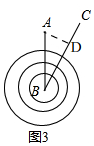 过A作AD⊥BC于D.在Rt△ABD中,
过A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=200,
∴AD=$\frac{1}{2}$AB=100,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为20×(12-4)=160.
∵100<160,
∴该城市会受到这次台风的影响;
∴该城市受到这次台风最大风力为:12-(100÷20)=7(级).
点评 此题是几何变换综合题,主要考查了折叠的性质,勾股定理的应用,解本题的关键是由折叠得出含30°的直角三角形性质,将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,使问题解决.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:填空题
 如图所示,长方形OABC的顶点A在x轴上,C在y轴上,点B坐标为(4,2),若直线y=mx-1恰好将长方形分成面积相等的两部分,则m的值为1.
如图所示,长方形OABC的顶点A在x轴上,C在y轴上,点B坐标为(4,2),若直线y=mx-1恰好将长方形分成面积相等的两部分,则m的值为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
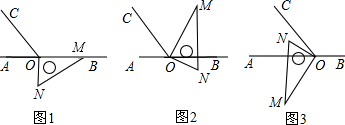
 如图,AC分别切⊙O于D、E,作OQ⊥BC交⊙O于P,连DP、EP交BC于G、F,AF、AG分别交DG、EF于M、N.求证:OQ⊥MN.
如图,AC分别切⊙O于D、E,作OQ⊥BC交⊙O于P,连DP、EP交BC于G、F,AF、AG分别交DG、EF于M、N.求证:OQ⊥MN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
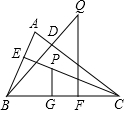 已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com