
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪��A��0��4![]() ������B��x�������ϣ�����ABO=30�ȣ�����P���߶�AB�ϴӵ�A���B��ÿ��
������B��x�������ϣ�����ABO=30�ȣ�����P���߶�AB�ϴӵ�A���B��ÿ��![]() ����λ���ٶ��˶������˶�ʱ��Ϊt�룮��x����ȡ����M��N���ȱ���PMN��
����λ���ٶ��˶������˶�ʱ��Ϊt�룮��x����ȡ����M��N���ȱ���PMN��
��1����ֱ��AB�Ľ���ʽ��
��2����ȱ���PMN�ı߳�����t�Ĵ���ʽ��ʾ������������ȱ���PMN�Ķ���M�˶�����ԭ��O�غ�ʱt��ֵ��
��3�����ȡOB���е�D����ODΪ����Rt��AOB�ڲ�����ͼ2��ʾ�ľ���ODCE����C���߶�AB�ϣ���ȱ���PMN�;���ODCE�ص����ֵ����ΪS���������0��t��2��ʱS��t�ĺ�����ϵʽ�������S�����ֵ��

���𰸡�(1) y=��![]() x+4
x+4![]() (2) PM=8��t��t=2 (3)��0��t��1ʱ��S=2
(2) PM=8��t��t=2 (3)��0��t��1ʱ��S=2![]() t+6
t+6![]() ����1��t��2ʱ��S=��2
����1��t��2ʱ��S=��2![]() t2+6
t2+6![]() t+4
t+4![]() ����t=2ʱ��S=8
����t=2ʱ��S=8![]() �����ֵΪ
�����ֵΪ![]()
��������
��1��������֪������õ�B�����꣬���ô���ϵ������ֱ��AB�ý���ʽ���ɣ���2����Rt��AOB�У����AB=8![]() �����ɱ�ʾ��BP= 8
�����ɱ�ʾ��BP= 8![]() -
-![]() t������tan��PBM=
t������tan��PBM=![]() ��������t�Ĵ���ʽ��ʾPM�ó�������M���O�غ�ʱ���ɵ�AO=2AP���ɴ˼������tֵ����3�����ݵ�0��t��1ʱ����1��t��2ʱ����t=2ʱ���ֱ����S��t�ĺ�������ʽ����������ֵ���Ƚϼ���.
��������t�Ĵ���ʽ��ʾPM�ó�������M���O�غ�ʱ���ɵ�AO=2AP���ɴ˼������tֵ����3�����ݵ�0��t��1ʱ����1��t��2ʱ����t=2ʱ���ֱ����S��t�ĺ�������ʽ����������ֵ���Ƚϼ���.
��1����OA=4![]() ����ABO=30�����õ�OB=12��
����ABO=30�����õ�OB=12��
��B��12��0������ֱ��AB����ʽΪy=kx+b��
��A��B�������ã�![]() ��
��
��ã�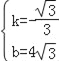 ��
��
��ֱ��AB�Ľ���ʽΪ��y=��![]() x+4
x+4![]() ��
��
��2���ߡ�AOB=90�㣬��ABO=30�㣬
��AB=2OA=8![]() ��
��
��AP=![]() t��
t��
��BP=AB��AP=8![]() t��
t��
�ߡ�PMN�ǵȱ������Σ�
���MPB=90�㣬
��tan��PBM=![]() ��
��
��PM=��8![]() ��
��![]() t����
t����![]() =8��t��
=8��t��
��ͼ1����P�ֱ���PQ��y����Q��PS��x����S��
�����AQ=![]() AP=
AP=![]() t��PS=QO=4
t��PS=QO=4![]() ��
��![]() t��
t��
��PM=��4![]() ��
��![]() ����
����![]() =8��t��
=8��t��
����M���O�غ�ʱ��
�ߡ�BAO=60�㣬
��AO=2AP��
��4![]() =2
=2![]() t��
t��
��t=2��

��3���ٵ�0��t��1ʱ����ͼ2��
��PN��EC�ڵ�G���ص�����Ϊֱ������EONG����GH��OB��H��
�ߡ�GNH=60�㣬![]() ��
��
��HN=2��
��PM=8��t��
��BM=16��2t��
��OB=12��
��ON=��8��t������16��2t��12��=4+t��
��OH=ON��HN=4+t��2=2+t=EG��
��S=![]() ��2+t+4+t����2
��2+t+4+t����2![]() =2
=2![]() t+6
t+6![]() ��
��
��S��t�����������
�൱t=1ʱ��Smax=8![]() ��
��
�ڵ�1��t��2ʱ����ͼ3��
��PM��EC�ڵ�I����EO�ڵ�F��PN��EC�ڵ�G���ص�����Ϊ�����OFIGN��
��GH��OB��H��
��FO=4![]() ��2
��2![]() t��
t��
��EF=2![]() ����4
����4![]() ��2
��2![]() t��=2
t��=2![]() t��2
t��2![]() ��
��
��EI=2t��2��
��S=S����ONGE��S��FEI=2![]() t+6
t+6![]() ��
��![]() ��2t��2����2
��2t��2����2![]() t��2
t��2![]() ��=��2
��=��2![]() t2+6
t2+6![]() t+4
t+4![]()
������ɵ�MO=4��2t��OF=��4��2t����![]() ��PC=4
��PC=4![]() ��
��![]() t��PI=4��t��
t��PI=4��t��
�ټ���S��FMO=![]() ��4��2t��2��
��4��2t��2��![]()
S��PMN=![]() ��8��t��2��S��PIG=
��8��t��2��S��PIG=![]() ��4��t��2��
��4��t��2��
��S=S��PMN��S��PIG��S��FMO=![]() ��8��t��2��
��8��t��2��![]() ��4��t��2��
��4��t��2��![]() ��4��2t��2��
��4��2t��2��![]()
=��2![]() t2+6
t2+6![]() t+4
t+4![]()
����2![]() ��0��
��0��
�൱![]() ʱ��S�����ֵ��Smax=
ʱ��S�����ֵ��Smax=![]() ��
��
�۵�t=2ʱ��MP=MN=6����N��D�غϣ�
��PM��EC�ڵ�I��PD��EC�ڵ�G���ص���
��Ϊ��������IMNG����ͼ4��S=![]() ��62��
��62��![]() ��22=8
��22=8![]() ��
��
������������0��t��1ʱ��S=2![]() t+6
t+6![]() ��
��
��1��t��2ʱ��S=��2![]() t2+6
t2+6![]() t+4
t+4![]() ��
��
��t=2ʱ��S=8![]() ��
��

��![]() ��
��
��S�����ֵ�� ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
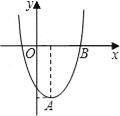
����Ŀ����ֱ������ƽ���ڣ����κ���ͼ��Ķ���ΪA��1����4�����ҹ���B��3��0����
��1����ö��κ����Ľ���ʽ��
��2�����ö��κ���ͼ������ƽ�Ƽ�����λ����ʹƽ�ƺ�����ͼ������ԭ�㣿��ֱ��д��ƽ�ƺ�����ͼ����x�����һ����������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��![]() (mΪ��������m��5)��
(m��������m��5)��
(1)������ͼ���ÿ����֧�ϣ�y��x�������������m��ȡֵ��Χ��
(2)����ͼ����һ�κ���y����x��1��ͼ���һ���������������3����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ʻʱ�ĺ�����Ϊ0.1��/ǧ�ף���ͼ������ʣ������![]() ���������ڼ����ͺ�����ʻ��·��
���������ڼ����ͺ�����ʻ��·��![]() ��ǧ�ף��ĺ���ͼ��.
��ǧ�ף��ĺ���ͼ��.

��1������ͼ��ֱ��д��������ʻ400ǧ��ʱ�������ڵ�ʣ�������������������ʱ�����������
��2����![]() ����
����![]() �ĺ�����ϵʽ���������������ʣ������5��ʱ������ʻ��·��.
�ĺ�����ϵʽ���������������ʣ������5��ʱ������ʻ��·��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=4��BC=6����B=60�㣬����ABC������BC�ķ���ƽ�ƣ��õ���A��B��C�䣬�ٽ���A��B��C���Ƶ�A����ʱ����תһ���ǶȺ�B��ǡ�����C�غϣ���ƽ�Ƶľ������ת�ǵĶ����ֱ�Ϊ��������

A��4��30�� B��2��60�� C��1��30�� D��3��60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ʷ��и߿��ڼ䣬ij�ľߵ�ƽ��ÿ�������![]() ֧
֧![]() Ǧ�ʣ�����
Ǧ�ʣ�����![]() ֧Ǧ�ʵ�������
֧Ǧ�ʵ�������![]() Ԫ�������鷢�֣����۵��ۚ���
Ԫ�������鷢�֣����۵��ۚ���![]() Ԫ��ÿ��ɶ�����
Ԫ��ÿ��ɶ�����![]() ֧Ǧ�ʣ�Ϊ��ʹÿ���ȡ��������࣬���ľߵ���������۵����½�
֧Ǧ�ʣ�Ϊ��ʹÿ���ȡ��������࣬���ľߵ���������۵����½�![]() Ԫ
Ԫ![]()
![]() ���۵����½�
���۵����½�![]() Ԫ���ľߵ�ƽ��ÿ�������________֧Ǧ�ʣ�������Ϊ________Ԫ��
Ԫ���ľߵ�ƽ��ÿ�������________֧Ǧ�ʣ�������Ϊ________Ԫ��
![]() �ڲ������������ص������£���
�ڲ������������ص������£���![]() ��Ϊ����Ԫʱ������ʹ���ľߵ�ÿ����
��Ϊ����Ԫʱ������ʹ���ľߵ�ÿ����![]() Ǧ�ʻ�ȡ������Ϊ
Ǧ�ʻ�ȡ������Ϊ![]() Ԫ��
Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η���![]() ,����˵��:����a+c=0,����
,����˵��:����a+c=0,����![]() ���������ȵ�ʵ����;��������
���������ȵ�ʵ����;��������![]() ���������ȵ�ʵ����,��
���������ȵ�ʵ����,��![]() Ҳһ�����������ȵ�ʵ����;����c�Ƿ���
Ҳһ�����������ȵ�ʵ����;����c�Ƿ���![]() ��һ����,��һ����
��һ����,��һ����![]() ����;����m�Ƿ���
����;����m�Ƿ���![]() ��һ����,��һ����
��һ����,��һ����![]() ����.������ȷ��ֻ�� �� ��
����.������ȷ��ֻ�� �� ��
A. �٢� B. �ڢ� C. �ۢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���μ䣬С��������ʦ�ĵ���ֱ�����ǰ��棬��С�ĵ�����ǽ֮�䣬��ͼ![]() ��
��![]() ��
��
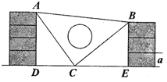
��1����֤��![]() ��
��
��2�������ǰ��һ��ֱ�DZ�![]() �������С�������ǽש��ĺ��a�Ĵ�С��ÿ��ש�ĺ����ȣ���
�������С�������ǽש��ĺ��a�Ĵ�С��ÿ��ש�ĺ����ȣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ֱ�������� CDE ���� CD=2 �� x ���ϣ���ECD=45������������ CDE �Ƶ� C ��ʱ����ת 75������ E �Ķ�Ӧ�� N ǡ������ y ���ϣ���� N ������Ϊ�� ��

A. ��0,3�� B. ��0,2![]() �� C. ��0,
�� C. ��0, ![]() �� D. ��0,
�� D. ��0, ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com