练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，等腰直角三角形 CDE 的腰 CD=2 在 x 轴上，∠ECD=45°，将三角形 CDE 绕点 C 逆时针旋转 75°，点 E 的对应点 N 恰好落在 y 轴上，则点 N 的坐标为（ ）

    A. （0,3） B. （0,2） C. （0, ） D. （0, ）

    【答案】C

    【解析】

    根据旋转得出∠NCE=75°，求出∠NCO，由 CD=2,利用勾股定理求出 CE 的长即为 CN 的长，即 可求出 ON 的长度

    ∵将三角形 CDE 绕点 C 逆时针旋转 75°，点 E 的对应点 N 恰好落在 OA 上，

    ∴∠ECN=75°，

    ∵∠ECD=45°，

    ∴∠NCO=180°﹣75°﹣45°=60°，

    ∵AO⊥OB，

    ∴∠AOB=90°，

    ∴∠ONC=30°，

    ∵等腰直角三角形DCE 旋转到△CMN，

    ∴△CMN 也是等腰直角三角形，

    ∵CM=2，

    ∴CN=2，

    ∴OC=

    ∴ON=

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，已知点A（0，4），点B在x正半轴上，且∠ABO=30度．动点P在线段AB上从点A向点B以每秒个单位的速度运动，设运动时间为t秒．在x轴上取两点M，N作等边△PMN．

    （1）求直线AB的解析式；

    （2）求等边△PMN的边长（用t的代数式表示），并求出当等边△PMN的顶点M运动到与原点O重合时t的值；

    （3）如果取OB的中点D，以OD为边在Rt△AOB内部作如图2所示的矩形ODCE，点C在线段AB上．设等边△PMN和矩形ODCE重叠部分的面积为S，请求出当0≤t≤2秒时S与t的函数关系式，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算下列各式，然后回答问题

    (x+4)(x+3)=

    (x+4)(x-3)=

    (x-4)(x+3)=

    (x-4)(x-3)=

    （1）有上面各式总结规律：一般地，(x+p)(x+q)=

    （2）运用上述规律，直接写出下式的结果：(x-199)(x+201)=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

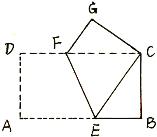
    【题目】如图，将长方形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕．

    （1）求证：△FGC≌△EBC；

    （2）试判断△CEF的形状，并证明你的结论；

    （3）若AB=8，AD=4，求四边形ECGF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示,△ABC中,∠B=90，AB=6cm，BC=8cm.

    (1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发.

    ①经过几秒,使△PBQ的面积等于8?

    ②线段PQ能否将△ABC分成面积相等的两部分?若能，求出运动时间；若不能说明理由.

    (2)若P点沿射线AB方向从A点出发以1cm/s的速度移动，点Q沿射线CB方向从C点出发以2cm/s的速度移动，P，Q同时出发，问几秒后，△PBQ的面积为1?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，∠ABC=25°，O为AB的中点. 将OA绕点O逆时针旋转θ °至OP（0<θ<180），当△BCP恰为轴对称图形时，θ的值为_____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为养成学生课外阅读的习惯，各学校普遍开展了“我的梦.中国梦”课外阅读活动．某校为了解七年级1200名学生课外日阅读所用时间情况，从中随机抽查了部分同学，进行了相关统计，整理并绘制出如下不完整的频数分布表和频数分布直方图，请根据图表信息解答下列问题：

    （1）表中 a= ，b= ；

    （2）请补全频数分布直方图中空缺的部分；

    （3）样本中，学生日阅读所用时间的中位数落在第 组；

    （4）请估计该校七年级学生日阅读量不足 1 小时的人数．

    组别

    时间段（小时）

    频数

    频率

    1

    0≤x＜0.5

    10

    0.05

    2

    0.5≤x＜1.0

    20

    0.10

    3

    1.0≤x＜1.5

    80

    b

    4

    1.5≤x＜2.0

    a

    0.35

    5

    2.0≤x＜2.5

    12

    0.06

    6

    2.5≤x＜3.0

    8

    0.04

    查看答案和解析>>

    科目：初中数学 来源： 题型：

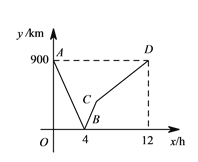
    【题目】一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为，两车之间的距离为，图中的折线表示与之间的函数关系，根据图象进行一下探究：

    信息读取（1）甲、乙两地之间的距离为______：

    （2）请解释图中点的实际意义：_______

    图象理解（3）求慢车和快车的速度：

    （4）求线段所表示的与之间的函数关系式，并写出自变量的取值范围：

    问题解决（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同，在第一列快车与慢车相遇分钟后，第二列快车与慢车相遇，求第二列快车比第一列快车晚出发多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如下图所示，直线y＝－x＋3与坐标轴分别交于点A，B，与直线y＝x交于点C，线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动，运动时间为t秒，连结CQ.

    (1)求出点C的坐标；

    (2)若△OQC是等腰直角三角形，则t的值为________；

    (3)若CQ平分△OAC的面积，求直线CQ对应的函数表达式．

    查看答案和解析>>

    同步练习册答案