
【题目】如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:

(1)画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(2)结合你的示意图,写出求电线杆高度的思路.
【答案】(1)画图见解析;(2)解法见解析.
【解析】
试题分析:(1)根据题意,设计方案如图,选用的测量工具:高为1.5m的测角仪,皮尺;
(2)根据正切函数进行设计测量方法,先测得CA的大小,因为四边形ACDE是矩形;可得DE=AC,AE=CD=1.5;根据相正切函数求得BE,即AB=BE+1.5.
试题解析:(1)测量方案示意图如图;选用的测量工具:高为1.5m的测角仪,皮尺;
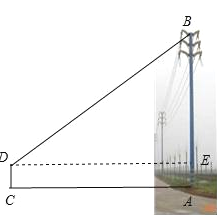
(2)CA(测角仪离电线杆的距离)=a,DC测角仪的高=1.5m,∠BDE(测角仪测的仰角)=α,
根据正切函数;可得:tanα=![]() ;
;
因为DE=CA=a(m),AE=CD=1.5m,
即BE=tanαa(m),
则AB=BE+AE=(tanαa+1.5)m.
故电线杆高度为(tanαa+1.5)米


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD与等边△AEF的边长相等,且E、F分别在BC、CD,则∠BAD的度数是( )
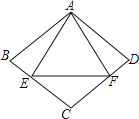
A.80° B.90° C.100° D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中与a-b-c的值不相等的是( )
A. a -(b + c) B. a -(b-c)
C. (a-b)+(-c) D. (-c)-(b-a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左边到右边的变形,是因式分解的是( )
A. (3-x)(3+x)=9-x2 B. m4-n4=(m2+n2)(m+n)(m-n)
C. (y+1)(y-3)=-(3-y)(y+1) D. 4yz-2y2z+z=2y(2z-yz)+z
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com