
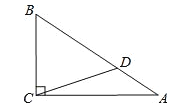
【题目】如图,Rt△ABC中,∠ACB=90°,cosA=![]() ,D为AB上一点,且AD:BD=1:2,若BC=3
,D为AB上一点,且AD:BD=1:2,若BC=3![]() ,求CD的长.
,求CD的长.
【答案】![]() .
.
【解析】
试题分析:过D作DE⊥AC于E,则DE∥BC.先在Rt△ABC中,由cosA=![]() ,可设AC=5k,则AB=6k,利用勾股定理得出AB2﹣AC2=BC2,求出k=±3(负值舍去),那么AC=15,AB=18.再由DE∥BC,得出
,可设AC=5k,则AB=6k,利用勾股定理得出AB2﹣AC2=BC2,求出k=±3(负值舍去),那么AC=15,AB=18.再由DE∥BC,得出![]() ,求出DE=
,求出DE=![]() BC=
BC=![]() ,AE=
,AE=![]() AC=5,CE=AC﹣AE=10,然后利用勾股定理得出CD=
AC=5,CE=AC﹣AE=10,然后利用勾股定理得出CD=![]() .
.
试题解析:过D作DE⊥AC于E,则DE∥BC.
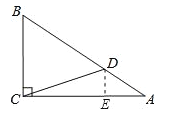
∵Rt△ABC中,∠ACB=90°,
∴cosA=![]() ,
,
∴设AC=5k,则AB=6k,
∵AB2﹣AC2=BC2,
∴36k2﹣25k2=99,
∴k=±3(负值舍去),
∴AC=15,AB=18.
∵DE∥BC,
∴![]() ,
,
∴DE=![]() BC=
BC=![]() ,AE=
,AE=![]() AC=5,
AC=5,
∴CE=AC﹣AE=10,
∴CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 调查市场上老酸奶的质量情况
B. 调查某品牌圆珠笔芯的使用寿命
C. 调查乘坐飞机的旅客是否携带了危禁物品
D. 调查我市市民对伦敦奥运会吉祥物的知晓率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,E为BD上的一点,连接EA,将EA绕点E逆时针旋转90°得线段EF,连接FB.

(1)如图a,点E在OB上,
①求∠FEB+∠BAE的度数;
②求证:ED﹣EB=![]() BF;
BF;
(2)如图b,当E在OD上时,按已知条件补全图形,直接写出ED、EB、BF三条线段的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
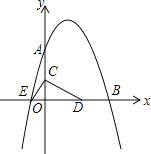
(1)求该抛物线的解析式及点E的坐标;
(2)若D点运动的时间为t,△CED的面积为S,求S关于t的函数关系式,并求出△CED的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:

(1)画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(2)结合你的示意图,写出求电线杆高度的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
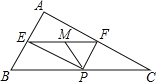
A.1.2 B.1.3 C.1.4 D.2.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com