
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
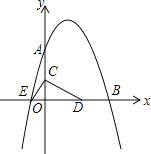
(1)求该抛物线的解析式及点E的坐标;
(2)若D点运动的时间为t,△CED的面积为S,求S关于t的函数关系式,并求出△CED的面积的最大值.
【答案】(1)y=﹣![]() x2+3x+8,E(﹣2,0);(2)当t=5时,S最大=
x2+3x+8,E(﹣2,0);(2)当t=5时,S最大=![]() .
.
【解析】
试题分析:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣![]() x2+bx+c即可求出抛物线的解析式为:y=﹣
x2+bx+c即可求出抛物线的解析式为:y=﹣![]() x2+3x+8;再令y=0,得:﹣
x2+3x+8;再令y=0,得:﹣![]() x2+3x+8=0,解方程可得点E的坐标;
x2+3x+8=0,解方程可得点E的坐标;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,然后由点A(0,8)、B(8,0),可得OA=8,OB=8,从而可得OD=8﹣t,然后令y=0,点E的坐标为(﹣2,0),进而可得OE=2,DE=2+8﹣t=10﹣t,然后利用三角形的面积公式即可求△CED的面积S与D点运动时间t的函数解析式为:S=﹣![]() t2+5t,然后转化为顶点式即可求出最值为:S最大=
t2+5t,然后转化为顶点式即可求出最值为:S最大=![]() .
.
解:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣![]() x2+bx+c得:
x2+bx+c得: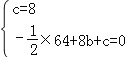 ,
,
解得:b=3,c=8,
故抛物线的解析式为:y=﹣![]() x2+3x+8,
x2+3x+8,
∵点A(0,8)、B(8,0),
∴OA=8,OB=8,
令y=0,得:﹣![]() x2+3x+8=0,
x2+3x+8=0,
解得:x1=8,x2=﹣2,
∵点E在x轴的负半轴上,
∴点E(﹣2,0),
∴OE=2;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8﹣t,
∴DE=OE+OD=10﹣t,
∴S=![]() DEOC=
DEOC=![]() (10﹣t)t=﹣
(10﹣t)t=﹣![]() t2+5t,
t2+5t,
即S=﹣![]() t2+5t=﹣
t2+5t=﹣![]() (t﹣5)2+
(t﹣5)2+![]() ,
,
∴当t=5时,S最大=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
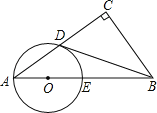
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
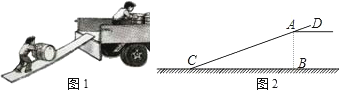
【题目】如图1,是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,则木板CD的长度为 .
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中与a-b-c的值不相等的是( )
A. a -(b + c) B. a -(b-c)
C. (a-b)+(-c) D. (-c)-(b-a)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com