
【题目】如图,已知![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 与
与![]() 平行的直线交射线
平行的直线交射线![]() 于点
于点![]() .
.
(1)当![]() ,
,![]() ,
,![]() 三点在同一直线上时(如图1),求证:
三点在同一直线上时(如图1),求证:![]() 为
为![]() 的中点;
的中点;

(2)将图1中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() ,
,![]() ,
,![]() 三点在同一直线上时(如图2),求证:
三点在同一直线上时(如图2),求证:![]() 为等腰直角三角形;
为等腰直角三角形;
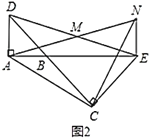
(3)将图1中![]() 绕点
绕点![]() 旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.

【答案】(1)证明见解析;(2)证明见解析;(3)成立,证明见解析.
【解析】
(1)利用ASA证明![]() ,可得
,可得![]() ,易证结论;
,易证结论;
(2)由![]() 及
及![]() 、
、![]() 为等腰直角三角形的性质可得
为等腰直角三角形的性质可得![]() ,
,![]() ,
,![]() ,由SAS可证
,由SAS可证![]() ,由全等三角形的性质易证
,由全等三角形的性质易证![]() 为等腰直角三角形;
为等腰直角三角形;
(3)由![]() 及
及![]() 、
、![]() 为等腰直角三角形的性质可得
为等腰直角三角形的性质可得![]() ,
,![]() ,由直角三角形两锐角互余及三角形内角和定理可知
,由直角三角形两锐角互余及三角形内角和定理可知![]() ,利用
,利用![]() 证明
证明![]() ,由全等三角形的性质易证
,由全等三角形的性质易证![]() 为等腰直角三角形.
为等腰直角三角形.
证明:(1)∵![]()
∴![]() (两直线平行,内错角相等)
(两直线平行,内错角相等)
∵点![]() 为
为![]() 的中点
的中点
∴![]() ,在
,在![]() 和
和![]() 中
中
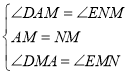
∴![]()
∴![]()
∴![]() 为
为![]() 的中点
的中点
(2)∵![]()
∴![]()
∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]() 且
且![]()
∴![]()
∵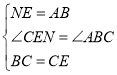
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 为等腰直角三角形
为等腰直角三角形
(3)(2)中的结论仍成立.
∵![]()
∴![]()
∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∵![]() ,
,![]()
![]() ,
,![]()
![]()
∴![]()
![]()
∴![]()
∵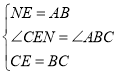
∴![]()
∴![]() ,
,![]()
∴![]()
∴![]() 为等腰直角三角形
为等腰直角三角形


科目:初中数学 来源: 题型:
【题目】中国扇文化有着深厚的文化底蕴,是民族文化的一个组成部分,它与竹文化、佛教文化有着密切关系.历来中国被誉为制扇王国.扇子主要材料是:竹、木、纸、象牙、玳瑁、翡翠、飞禽翎毛、其它棕榈叶、槟榔叶、麦杆、蒲草等也能编制成各种千姿百态的日用工艺扇,造型优美,构造精制,经能工巧匠精心镂、雕、烫、钻或名人挥毫题诗作画,使扇子艺术身价倍增.折扇,古称“聚头扇“,或称为撒扇,或折叠扇,以其收拢时能够二头合并归一而得名.如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,求出扇面的面积(用代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
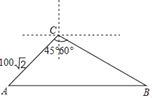
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数)
≈1.73,计算结果保留两位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:设a+
)2,善于思考的小明进行了以下探索:设a+![]() b=(m+
b=(m+![]() n)2(其中a,b,m,n均为正整数),则有a+
n)2(其中a,b,m,n均为正整数),则有a+![]() b=m2+2n2+2
b=m2+2n2+2![]() mn,∴a=m2+2n2,b=2mn.这样小明就找到了一种把a+
mn,∴a=m2+2n2,b=2mn.这样小明就找到了一种把a+![]() b化为平方式的方法.
b化为平方式的方法.
请你仿照小明的方法探索并解决下列问题.
(1)当a、b、m、n均为正整数时,若a+![]() b=(m+
b=(m+![]() n)2,用含m、n的式子分别表示a、b,则a= ,b= ;
n)2,用含m、n的式子分别表示a、b,则a= ,b= ;
(2)求7+4![]() 的算术平方根.
的算术平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
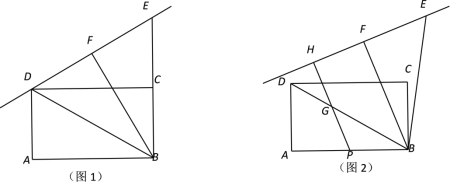
【题目】已知,在矩形ABCD中,BC=2,连接BD,把△ABD绕点B顺时针旋转后得到△FBE,旋转角度小于360°.
(1)如图1,当点E在BC的延长线上,且直线EF过点D,求AB的长.
(2)若AB=4,如图2,取AB边的中点P,过点P作直线EF的垂线PH,垂足为H.
① 若PH交线段BD于点G,当△BPG为等腰三角形时,求BG的长;
② 直接写出PH长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
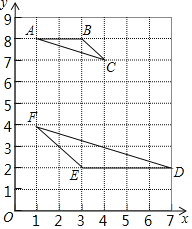
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点![]() 每个小方格的顶点叫格点
每个小方格的顶点叫格点![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
![]() 外接圆的圆心坐标是______;
外接圆的圆心坐标是______;
![]() 外接圆的半径是______;
外接圆的半径是______;
![]() 已知
已知![]() 与
与![]() 点D、E、F都是格点
点D、E、F都是格点![]() 成位似图形,则位似中心M的坐标是______;
成位似图形,则位似中心M的坐标是______;
![]() 请在网格图中的空白处画一个格点
请在网格图中的空白处画一个格点![]() ,使
,使![]() ∽
∽![]() ,且相似比为
,且相似比为![]() :1.
:1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,BC=6,AB=10.点Q与点B在AC的同侧,且AQ⊥AC.

(1)如图1,点Q不与点A重合,连结CQ交AB于点P.设AQ=x,AP=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)是否存在点Q,使△PAQ与△ABC相似,若存在,求AQ的长;若不存在,请说明理由;
(3)如图2,过点B作BD⊥AQ,垂足为D.将以点Q为圆心,QD为半径的圆记为⊙Q.若点C到⊙Q上点的距离的最小值为8,求⊙Q的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com