
【题目】已知抛物线y=ax2﹣2ax+c与x轴交于A,B两点(A在B左侧),与y轴正半轴交于点C,且满足:(1)一元二次方程ax2﹣2ax+c=0的一个解是﹣1;(2)抛物线的顶点在直线y=2x上.
问:(1)直接写出A、B两点的坐标.
(2)求此抛物线的解析式.
【答案】(1)A(﹣1,0),B(3,0);(2)![]() .
.
【解析】
(1)根据抛物线与x轴的交点坐标得抛物线与x轴的一个交点坐标为(﹣1,0),再求出抛物线的对称轴为直线x=1,然后利用对称性确定抛物线与x轴的另一个交点坐标;
(2)先确定抛物线的顶点坐标为(1,2),设顶点式y=a(x﹣1)2+2,然后把A点坐标代入求出a即可.
解:(1)∵一元二次方程ax2﹣2ax+c=0的一个解是﹣1,
∴抛物线与x轴的一个交点坐标为(﹣1,0),
∵抛物线的对称轴为直线![]() ,
,
∴抛物线与x轴的另一个交点的坐标为(3,0);
即A、B两点的坐标为:A(﹣1,0),B(3,0);
(2)∵抛物线的顶点在直线y=2x上,对称轴为直线![]()
∴抛物线的顶点坐标为(1,2),
设抛物线解析式为![]() ,
,
把A(﹣1,0)代入得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为![]() .
.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点O(0,0),P(1,2),将线段PO绕点P按顺时针方向以每秒90°的速度旋转,则第19秒时,点O的对应点坐标为( )
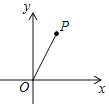
A.(0,0)B.(3,1)C.(﹣1,3)D.(2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A是y轴上一点,其坐标为(0,6),点B在x轴的正半轴上.点P,Q均在线段AB上,点P的横坐标为m,点Q的横坐标大于m,在△PQM中,若PM∥x轴,QM∥y轴,则称△PQM为点P,Q的“肩三角形.
(1)若点B坐标为(4,0),且m=2,则点P,B的“肩三角形”的面积为 ;
(2)当点P,Q的“肩三角形”是等腰三角形时,求点B的坐标;
(3)在(2)的条件下,作过O,P,B三点的抛物线y=ax2+bx+c
①若M点必为抛物线上一点,求点P,Q的“肩三角形”面积S与m之间的函数关系式,并写出自变量m的取值范围.
②当点P,Q的“肩三角形”面积为3,且抛物线y=ax2+bx+c与点P,Q的“肩三角形”恰有两个交点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.开通后从香港到珠海的车程由原来的180千米缩短到50千米,港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米,若开通后按设计时速行驶,行驶完全程时间仅为原来路程行驶完全程时间的![]() ,求港珠澳大桥的设计时速是多少.
,求港珠澳大桥的设计时速是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数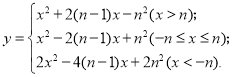 其中
其中![]() 是常数,且
是常数,且![]() >0.
>0.
(1)若点(![]() ,2)在函数的图象上,求
,2)在函数的图象上,求![]() 的值.
的值.
(2)当![]() =1时,①当
=1时,①当![]() ≤
≤![]() ≤2时,求函数值
≤2时,求函数值![]() 的取值范围.
的取值范围.
②当![]() ≤
≤![]() ≤
≤![]() 时,函数图象上的点到
时,函数图象上的点到![]() 轴的距离恒(永远)小于6,求
轴的距离恒(永远)小于6,求![]() 的取值范围.
的取值范围.
(3)直接写出函数图象与![]() 有两个交点时的
有两个交点时的![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
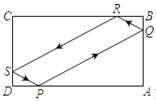
【题目】如图![]() 是一个矩形桌子,一小球从
是一个矩形桌子,一小球从![]() 撞击到
撞击到![]() ,反射到
,反射到![]() ,又从
,又从![]() 反射到
反射到![]() ,从
,从![]() 反射回原处
反射回原处![]() ,入射角与反射角相等(例如
,入射角与反射角相等(例如![]() 等),已知
等),已知![]() ,
,![]() ,
,![]() .则小球所走的路径的长为__________.
.则小球所走的路径的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
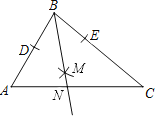
【题目】如图,在△ABC中,按以下步骤作图:①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;②分别以D,E为圆心,以大于![]() DE的同样长为半径作弧,两弧交于点M;③作射线BM交AC于N.如果BN=NC,∠A=57°,那么∠ABN的度数为_____.
DE的同样长为半径作弧,两弧交于点M;③作射线BM交AC于N.如果BN=NC,∠A=57°,那么∠ABN的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,顶点坐标
,顶点坐标![]() 与y轴交在
与y轴交在![]() ,
,![]() 之间(包含端点),则下列结论:①
之间(包含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于x的方程
总成立;④关于x的方程![]() 有两个不等的实根. 其中正确的个数是( )
有两个不等的实根. 其中正确的个数是( )
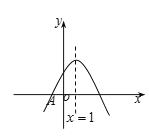
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
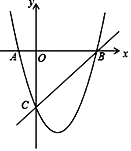
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com