
【题目】在平面直角坐标系中,点A是y轴上一点,其坐标为(0,6),点B在x轴的正半轴上.点P,Q均在线段AB上,点P的横坐标为m,点Q的横坐标大于m,在△PQM中,若PM∥x轴,QM∥y轴,则称△PQM为点P,Q的“肩三角形.
(1)若点B坐标为(4,0),且m=2,则点P,B的“肩三角形”的面积为 ;
(2)当点P,Q的“肩三角形”是等腰三角形时,求点B的坐标;
(3)在(2)的条件下,作过O,P,B三点的抛物线y=ax2+bx+c
①若M点必为抛物线上一点,求点P,Q的“肩三角形”面积S与m之间的函数关系式,并写出自变量m的取值范围.
②当点P,Q的“肩三角形”面积为3,且抛物线y=ax2+bx+c与点P,Q的“肩三角形”恰有两个交点时,直接写出m的取值范围.
【答案】(1)3;(2)(6,0);(3)①S=2m2﹣12m+18(0<m<3);②m=3﹣![]() 或3≤m≤6﹣
或3≤m≤6﹣![]() .
.
【解析】
(1)先利用待定系数法求出直线AB解析式,进而可得点P、M坐标,然后根据三角形的面积公式求解即可;
(2)根据题意可得MP=MQ,∠PMQ=90°,进而可得OB与OA的关系,问题即得解决;
(3)①因为M点必为抛物线上一点,所以可先确定自变量m取值范围,然后利用待定系数法求出直线AB的表达式,由抛物线y=ax2+bx+c经过O,B两点,根据抛物线的对称性可确定抛物线的对称轴,设出点P的坐标后即得点Q的坐标,进而可求得PM的长,进一步即可求出S与m之间的函数关系式;
②当点P在对称轴左侧,利用①中的关系式即可求出m的值;当点P在对称轴上或对称轴右侧时,由“肩三角形”面积为3可求出PQ的长,于是可用m的代数式表示出Q、M的坐标,进一步即得关于m的不等式组,解不等式组即得结果.
解:(1)如图1,∵A(0,6),B(4,0),
∴直线AB解析式为y=﹣![]() x+6,
x+6,
∵m=2,∴P(2,3),
∵PM∥x轴,BM∥y轴,
∴M(4,3),∠PMB=90°,
∴PM=2,BM=3,
∴点P,B的“肩三角形”△PBM的面积=![]() PMBM=
PMBM=![]() ×2×3=3;
×2×3=3;
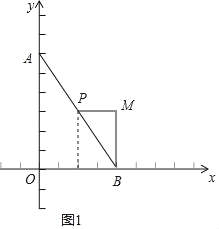
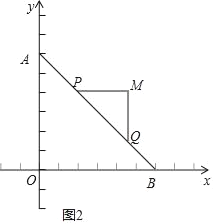
(2)如图2,根据题意,得MP=MQ,∠PMQ=90°,
∴∠MPQ=45°,
∴∠ABO=45°,
∴OB=OA=6,
∴点B的坐标为(6,0);
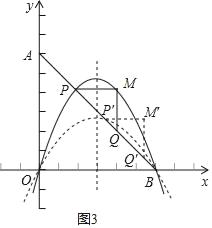
(3)如图3,①因为M点必为抛物线上一点,所以自变量m取值范围为:0<m<3,
由(2)易得,直线AB的表达式为y=6﹣x,
∴点P的坐标为(m,6﹣m),
∵抛物线y=ax2+bx+c经过O,B两点,
∴抛物线的对称轴为直线x=3,
∴点M的坐标为(6﹣m,6﹣m),
∴PM=(6﹣m)﹣m=6﹣2m,
S=![]() PM2=
PM2=![]() ×(6﹣2m)2=2m2﹣12m+18(0<m<3);
×(6﹣2m)2=2m2﹣12m+18(0<m<3);
②当点P在对称轴左侧,即0<<3时,∵点P,Q的“肩三角形”面积为3,
由①得:2m2﹣12m+18=3,解得:m=3﹣![]() (已舍去不合题意的);
(已舍去不合题意的);
当点P在对称轴上或对称轴右侧,即3≤m<6时,由点P,Q的“肩三角形”面积为3可得PM=![]() ,
,
∴M(m+![]() ,6﹣m),Q(m+
,6﹣m),Q(m+![]() ,6﹣
,6﹣![]() ﹣m)
﹣m)
∵抛物线=ax2+bx+c与点P,Q的“肩三角形”恰有两个交点,
∴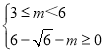 ,解得:3≤m≤6﹣
,解得:3≤m≤6﹣![]() ,
,
综上所述,m的取值范围为:m=3﹣![]() 或3≤m≤6﹣
或3≤m≤6﹣![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
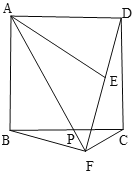
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用无刻度直尺作图(辅助线请画虚线)
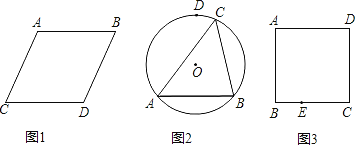
(1)如图1,在ABCD中画一条直线平分周长;
(2)如图2,在⊙O中,AB为⊙O内的一条弦,D为优弧AB的中点,C为优弧AB的一动点,画出∠ACB的平分线;
(3)如图3,在正方形ABCD中,E为CB上的任意一点,在AB上截取一点F,使得BF=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,连接OA、OB,若OA⊥OB,OB=OA,则k=_____.
的图象上,连接OA、OB,若OA⊥OB,OB=OA,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
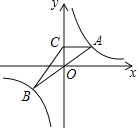
【题目】如图,一直线经过原点O,且与反比例函数y=![]() (k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=_____.
(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
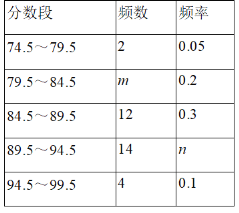
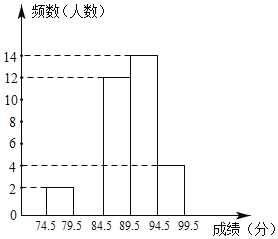
(1)表中m= ,n= ;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小雨利用几何画板探究函数y=![]() 图象,在他输入一组a,b,c的值之后,得到了如图所示的函数图象,根据学习函数的经验,可以判断,小雨输入的参数值满足( )
图象,在他输入一组a,b,c的值之后,得到了如图所示的函数图象,根据学习函数的经验,可以判断,小雨输入的参数值满足( )
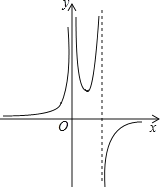
A.a>0,b>0,c=0B.a<0,b>0,c=0
C.a>0,b=0,c=0D.a<0,b=0,c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块直角三角板如图1放置,等腰直角三角板ABC的直角顶点是点A,AB=AC=3,直角板EDF的直角顶点D在BC上,且CD:BD=1:2,∠F=30°.三角板ABC固定不动,将三角板EDF绕点D逆时针旋转,旋转角为α(0°<α<90°).
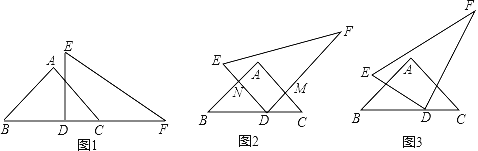
(1)当α= 时,EF∥BC;
(2)当α=45°时,三角板EDF绕点D逆时针旋转至如图2位置,设DF与AC交于点M,DE交AB于点N,求四边形ANDM的面积.
(3)如图3,设CM=x,四边形ANDM的面积为y,求y关于x的表达式(不用写x的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)过A(-1,1),B(3,1),C(-2,y1),D(2,y2)四点,则y1与y2的大小关系是( )
A.y1>y2B.y1=y2C.y1<y2D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com