
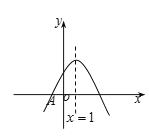
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,顶点坐标
,顶点坐标![]() 与y轴交在
与y轴交在![]() ,
,![]() 之间(包含端点),则下列结论:①
之间(包含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于x的方程
总成立;④关于x的方程![]() 有两个不等的实根. 其中正确的个数是( )
有两个不等的实根. 其中正确的个数是( )
A.1个B.2个C.3个D.4个
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
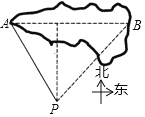
【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离.现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东α方向,测得点P与亭子A之间的距离为200米.则亭子A与亭子B之间的距离为( )
A.100+100![]() sinα米B.100+100
sinα米B.100+100![]() tanα米
tanα米
C.100+![]() 米D.100+
米D.100+![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2ax+c与x轴交于A,B两点(A在B左侧),与y轴正半轴交于点C,且满足:(1)一元二次方程ax2﹣2ax+c=0的一个解是﹣1;(2)抛物线的顶点在直线y=2x上.
问:(1)直接写出A、B两点的坐标.
(2)求此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
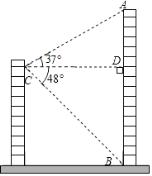
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈
,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈![]() ,cos53°≈0.60)
,cos53°≈0.60)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
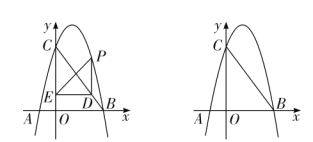
(1)求抛物线的解析式;
(2)点![]() 是抛物线上一点,设
是抛物线上一点,设![]() 点的横坐标为
点的横坐标为![]() .
.
①当点![]() 在第一象限时,过点
在第一象限时,过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() ,当
,当![]() 和
和![]() 相似时,求点
相似时,求点![]() 的坐标;
的坐标;
②请直接写出使![]() 的点
的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=BC,A、B的坐标分别为(0,4),(-2,4),将△ABC绕点P旋转180°后得到△A′B′C′,其中点B的对应点B′的坐标为(2,2).
(1)求出点C的坐标;
(2)求点P的坐标,并求出点C的对应点C′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是对称轴与
是对称轴与![]() 轴的交点.
轴的交点.
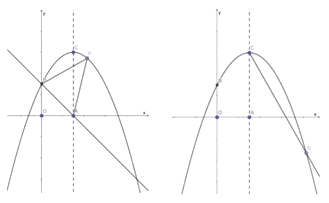
(1)求抛物线的解析式;
(2)如图①所示, ![]() 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求
是抛物线上的一个动点,且位于第一象限,连结BP、AP,求![]() 的面积的最大值;
的面积的最大值;
(3)如图②所示,在对称轴![]() 的右侧作
的右侧作![]() 交抛物线于点
交抛物线于点![]() ,求出
,求出![]() 点的坐标;并探究:在
点的坐标;并探究:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com