
【题目】如图所示,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是对称轴与
是对称轴与![]() 轴的交点.
轴的交点.
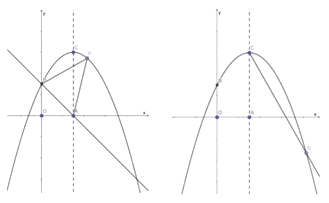
(1)求抛物线的解析式;
(2)如图①所示, ![]() 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求
是抛物线上的一个动点,且位于第一象限,连结BP、AP,求![]() 的面积的最大值;
的面积的最大值;
(3)如图②所示,在对称轴![]() 的右侧作
的右侧作![]() 交抛物线于点
交抛物线于点![]() ,求出
,求出![]() 点的坐标;并探究:在
点的坐标;并探究:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 最大值为
最大值为![]() ;(3)存在,
;(3)存在,![]() 点坐标为
点坐标为![]() ,理由见解析
,理由见解析
【解析】
(1)利用待定系数法可求出二次函数的解析式;
(2)求三角形面积的最值,先求出三角形面积的函数式.从图形上看S△PAB=S△BPO+S△APO-S△AOB,设P![]() 求出关于n的函数式,从而求S△PAB的最大值.
求出关于n的函数式,从而求S△PAB的最大值.
(3) 求点D的坐标,设D![]() ,过D做DG垂直于AC于G,构造直角三角形,利用勾股定理或三角函数值来求t的值即得D的坐标;探究在y轴上是否存在点
,过D做DG垂直于AC于G,构造直角三角形,利用勾股定理或三角函数值来求t的值即得D的坐标;探究在y轴上是否存在点![]() ,使
,使![]() ?根据以上条件和结论可知∠CAD=120°,是∠CQD的2倍,联想到同弧所对的圆周角和圆心角,所以以A为圆心,AO长为半径做圆交y轴与点Q,若能求出这样的点,就存在Q点.
?根据以上条件和结论可知∠CAD=120°,是∠CQD的2倍,联想到同弧所对的圆周角和圆心角,所以以A为圆心,AO长为半径做圆交y轴与点Q,若能求出这样的点,就存在Q点.
解:![]() 抛物线顶点为
抛物线顶点为![]()
![]() 可设抛物线解析式为
可设抛物线解析式为![]()
将![]() 代入
代入![]() 得
得
![]()
![]()
![]() 抛物线
抛物线![]() ,即
,即![]()
![]() 连接
连接![]() ,
,
![]()
设![]() 点坐标为
点坐标为![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 最大值为
最大值为![]()
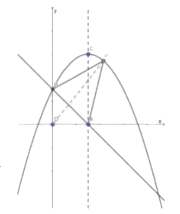
![]() 存在,设点D的坐标为
存在,设点D的坐标为![]()
过![]() 作对称轴的垂线,垂足为
作对称轴的垂线,垂足为![]() ,
,
则![]()
![]()
![]()
在![]() 中有
中有
![]()
![]()
化简得![]()
![]() (舍去),
(舍去),![]()
∴点D(![]() ,-3)
,-3)
![]()
连接![]() ,在
,在![]() 中
中
![]()
![]()
![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆与
为半径的圆与![]() 轴的交点上
轴的交点上
此时![]()
设![]() 点为(0,m), AQ为
点为(0,m), AQ为![]() 的半径
的半径
则AQ=OQ+OA, 6=m+3
即![]()
∴![]()
综上所述,![]() 点坐标为
点坐标为![]()
故存在点Q,且这样的点有两个点.


 培优口算题卡系列答案
培优口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,顶点坐标
,顶点坐标![]() 与y轴交在
与y轴交在![]() ,
,![]() 之间(包含端点),则下列结论:①
之间(包含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于x的方程
总成立;④关于x的方程![]() 有两个不等的实根. 其中正确的个数是( )
有两个不等的实根. 其中正确的个数是( )
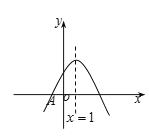
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
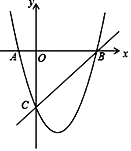
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣m)2+2m(m≠0)经过原点,其顶点为P,与x轴的另一交点为A.
(1)P点坐标为 ,A点坐标为 ;(用含m的代数式表示)
(2)求出a,m之间的关系式;
(3)当m>0时,若抛物线y=a(x﹣m)2+2m向下平移m个单位长度后经过点(1,1),求此抛物线的表达式;
(4)若抛物线y=a(x﹣m)2+2m向下平移|m|个单位长度后与x轴所截的线段长,与平移前相比有什么变化?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
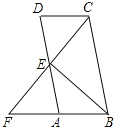
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=100°,求∠ABE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
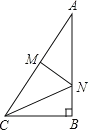
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则△BCN的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.
下列说法中错误的是
A. 红红不是胜就是输,所以红红胜的概率为![]()
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为![]()
D. 娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com