【题目】已知A(0，1)，B(2，0)，C(4，3)．
(1)在坐标系中描出各点，画出三角形ABC；
(2)求三角形ABC的面积；
(3)设点P在坐标轴上，且三角形ABP与三角形ABC的面积相等，请直接写出点P的坐标．
【答案】(1) 见解析；（2）4；（3）点P的坐标为(10，0)或(－6，0)或(0，5)或(0，－3)
【解析】分析：(1)、在平面直角坐标系中描出各点，从而得出三角形；(2)、利用矩形的面积减去三个直角三角形的面积得出△ABC的面积；(3)、根据三角形的面积得出三角形的底，从而得出点的坐标．
详解：(1)三角形ABC如图所示
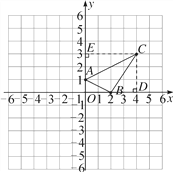
如图，过点C向x轴、y轴作垂线，垂足为D，E.
∴S长方形DOEC＝3×4＝12，S三角形BCD＝
×2×3＝3，
S三角形ACE＝×2×4＝4，S三角形AOB＝×2×1＝1，
∴S三角形ABC＝S长方形DOEC－S三角形ACE－S三角形BCD－S三角形AOB＝12－4－3－1＝4 ，
(3)点P的坐标为(10，0)或(－6，0)或(0，5)或(0，－3)
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】将2x2a-6xab+2x分解因式，下面是四位同学分解的结果：
①2x（xa-3ab）， ②2xa（x-3b+1）， ③2x（xa-3ab+1）， ④2x（-xa+3ab-1）．
其中，正确的是（ ）
A.①B.②C.③D.④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有许多代数恒等式可以用图形的面积来表示，如图①，它表示(2m+n)(m+n)=2m2+3mn+n2．
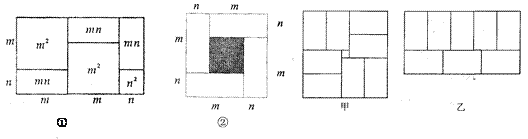
(1) 观察图②,请你写出三个代数式(m+n) 2、(m－n) 2、mn之间的等量关系是_________;
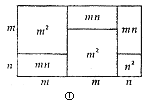
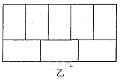
(2) 小明用8个一样大的长方形(长acm，宽bcm)拼图，拼出了如图甲、乙的两种图案：图案甲是一个正方形，图案乙是一个大的长方形：图案甲的中间留下了边长是2cm的正方形小洞．则(a+2b)2－8ab的值_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
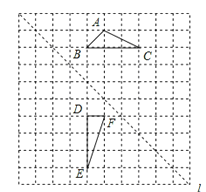
【题目】如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC和△DEF（顶点为网格线的交点），以及过格点的直线l．
①将△ABC向右平移两个单位长度，再向下平移两个单位长度，画出平移后的三角形△A’B’C’；
②画出△DEF关于直线l对称的三角形△D’E’F’；
③填空：∠C+∠E= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】当三角形中一个内角是另一个内角的3倍时，我们称此三角形为“梦想三角形”．如果一个“梦想三角形”有一个角为108°，那么这个“梦想三角形”的最小内角的度数为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
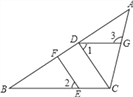
【题目】如图，在△ABC中，点E在BC上，CD⊥AB，EF⊥AB，垂足分别为D、F．
（1）CD与EF平行吗？为什么？
（2）如果∠1=∠2，且∠3=115°，求∠ACB的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
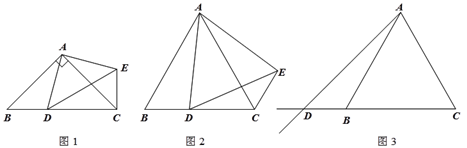
【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；
（2）设∠BAC= 
，∠DCE= 
．
① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究
与
之间的数量关系，并证明你的结论；
② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时
与
之间的数量关系（不需证明）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，△DEF是由△ABC绕点O顺时针旋转180°后形成的图形；
(1)请你指出图中所有相等的线段；
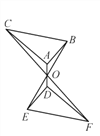
(2)图中哪些三角形可以被看成是关于点O成中心对称关系？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com