
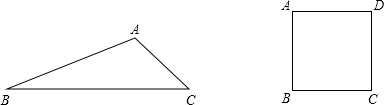
分析 ①因为∠A=120°,可以以A为顶点作∠BAP=20°,则∠PAC=100°,∠APC=40°,所以△APB,△APC都是等腰三角形;还可以以A为顶点作∠BAP=80°,则∠PAC=40°,∠APC=100°,所以△APB,△APC都是等腰三角形;
②根据正方形的性质可得,满足这样的点首先有:两条对角线的交点;再以四个顶点为圆心以边长为半径画圆,在正方形里面和外面的交点一共有8个.根据半径相等,这些点就是要求的点.
解答 解:①如图所示:
②如图所示:9个.两条对角线的交点是一个.
以四个顶点为圆心以边长为半径画圆,在正方形里面和外面的交点一共有8个.
这些点就是要求的点.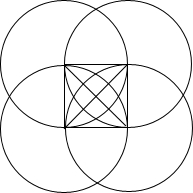
点评 本题主要考查了作图-应用与设计作图、等腰三角形的判定、正方形的性质以及作图,难度中等.确定分割三角形中的哪一个角是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
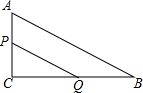 如图,Rt△ACB中,∠ACB=90°,AC=4,BC=10.点P、Q分别是两直角边CA、CB上的动点,点P以1个单位长度/秒的速度从点C运动向点A运动,点Q以2个单位长度/秒的速度从点C运动向点B即运动,当点P运动到点A时,两点均停止运动.设四边形APQB的面积为S,则S关于t的函数的图象大致是( )
如图,Rt△ACB中,∠ACB=90°,AC=4,BC=10.点P、Q分别是两直角边CA、CB上的动点,点P以1个单位长度/秒的速度从点C运动向点A运动,点Q以2个单位长度/秒的速度从点C运动向点B即运动,当点P运动到点A时,两点均停止运动.设四边形APQB的面积为S,则S关于t的函数的图象大致是( )| A. | 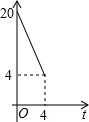 | B. | 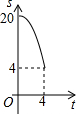 | C. | 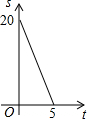 | D. | 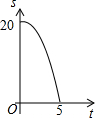 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com