
 如图,在梯形ABCD中,AD∥BC,AC与BD交于点O,若S△AOD=4,S△BOC=9,则S梯形ABCD=25.
如图,在梯形ABCD中,AD∥BC,AC与BD交于点O,若S△AOD=4,S△BOC=9,则S梯形ABCD=25. 分析 由梯形ABCD中AD∥BC,可得△AOD∽△COB,然后由相似三角形面积比等于相似比的平方,求得△BOC的面积,又由等高三角形的面积的比等于对应底的比,可求得△AOB与△COD的面积,继而求得答案.
解答 解:∵梯形ABCD中AD∥BC,
∴△AOD∽△COB,
∴S△AOD:S△BOC=4:9,
∴OA:OC=AD:BC=2:3,
∵S△AOD=4,S△BOC=9,
∴S△AOB=S△COD=$\frac{3}{2}$S△AOD=6,
∴梯形ABCD的面积为:S△AOD+S△AOB+S△BOC+S△COD=25.
故答案为:25.
点评 此题考查了梯形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
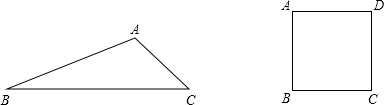
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
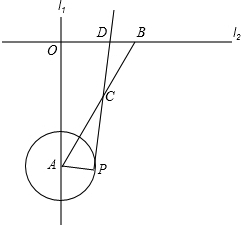 如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.
如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
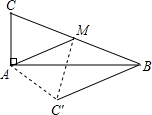 如图,在Rt△ABC中,∠BAC=90°,点M为斜边BC的中点,AM=5厘米,∠AMC=45°,将△AMC沿AM翻折,点C落在△ABC所在平面内的C′处,那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米.
如图,在Rt△ABC中,∠BAC=90°,点M为斜边BC的中点,AM=5厘米,∠AMC=45°,将△AMC沿AM翻折,点C落在△ABC所在平面内的C′处,那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天某地区早晨有雾 | |
| B. | 抛掷一枚质地均匀的骰子,向上一面的点数是6 | |
| C. | 一个不透明的袋子中有2个红球和1个白球,从中摸出1个球,该球是黑球 | |
| D. | 明天见到的第一辆公交车的牌照的末位数字将是偶数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com