
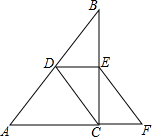
 已知:如图,在△ABC中,D,E分别是AB,BC的中点,点F在AC的延长线上,且CF=DE.求证:DC∥EF.
已知:如图,在△ABC中,D,E分别是AB,BC的中点,点F在AC的延长线上,且CF=DE.求证:DC∥EF.  名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:填空题
 如图,点A(m,2),B(5,n)在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,将该函数图象向上平移2个单位长度得到一条新的曲线,点A、B的对应点分别为A′、B′.图中阴影部分的面积为8,则k的值为2.
如图,点A(m,2),B(5,n)在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,将该函数图象向上平移2个单位长度得到一条新的曲线,点A、B的对应点分别为A′、B′.图中阴影部分的面积为8,则k的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
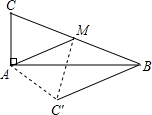 如图,在Rt△ABC中,∠BAC=90°,点M为斜边BC的中点,AM=5厘米,∠AMC=45°,将△AMC沿AM翻折,点C落在△ABC所在平面内的C′处,那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米.
如图,在Rt△ABC中,∠BAC=90°,点M为斜边BC的中点,AM=5厘米,∠AMC=45°,将△AMC沿AM翻折,点C落在△ABC所在平面内的C′处,那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
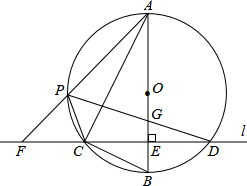 如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天某地区早晨有雾 | |
| B. | 抛掷一枚质地均匀的骰子,向上一面的点数是6 | |
| C. | 一个不透明的袋子中有2个红球和1个白球,从中摸出1个球,该球是黑球 | |
| D. | 明天见到的第一辆公交车的牌照的末位数字将是偶数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com