
如图:在数轴上 A 点表示数 a,B 点示数 b,C 点表示数 c,b 是最小的正整数,且 a、b 满足|a+2|+
(c﹣7)2=0.

(1)a= ,b= ,c= ;
若将数轴折叠,使得 A 点与 C 点重合,则点 B 与数 表示的点重合;
(3)点 A、B、C 开始在数轴上运动,若点 A 以每秒 1 个单位长度的速度向左运动,同时,点 B 和 点 C 分别以每秒 2 个单位长度和 4 个单位长度的速度向右运动,假设 t 秒钟过后,若点 A 与点 B 之 间的距离表示为 AB,点 A 与点 C 之间的距离表示为 AC,点 B 与点 C 之间的距离表示为 BC.则 AB= ,AC= ,BC= .(用含 t 的代数式表示)
(4)请问:3BC﹣2AB 的值是否随着时间 t 的变化而改变?若变化,请说明理由;若不变,请求其 值.
【考点】数轴;两点间的距离.
【分析】(1)利用|a+2|+(c﹣7)2=0,得 a+2=0,c﹣7=0,解得 a,c 的值,由 b 是最小的正整数, 可得 b=1;
先求出对称点,即可得出结果;
(3)由 3BC﹣2AB=3﹣2(3t+3)求解即可.
【解答】解:(1)∵|a+2|+(c﹣7)2=0,
∴a+2=0,c﹣7=0, 解得 a=﹣2,c=7,
∵b 是最小的正整数,
∴b=1; 故答案为:﹣2,1,7.
(7+2)÷2=4.5,
对称点为 7﹣4.5=2.5,2.5+=4; 故答案为:4.
(3)AB=t+2t+3=3t+3,AC=t+4t+9=5t+9,BC=2t+6;
故答案为:3t+3,5t+9,2t+6.
(4)不变.
3BC﹣2AB=3﹣2(3t+3)=12.
【点评】本题主要考查了数轴及两点间的距离,解题的关键是利用数轴的特点能求出两点间的距离


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
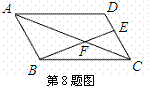
如图,在平行四边形ABCD 中,点E在CD上,若DE︰CE =1︰2,
则△CEF与△ABF的周长比为( ).
A.1︰2 B.1︰3 C.2︰3 D.4︰9
查看答案和解析>>
科目:初中数学 来源: 题型:
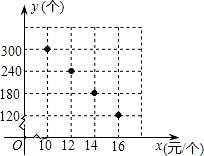
在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得 利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量 y(个)与销售单价 x(元/个) 之间的对应关系如图所示:
(1)试判断 y 与 x 之间的函数关系,并求出函数关系式;
若许愿瓶的进价为 6 元/个,按照上述市场调查的销售规律,求销售利润 w(元)与销售单价 x(元/
个)之间的函数关系式;
(3)在的条件下,若许愿瓶的进货成本不超过 900 元,要想获得最大利润,试确定这种许愿瓶的销 售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
一次函数 y=x+5 的图象经过点 P(a,b)和 Q(c,d),则 a(c﹣d)﹣b(c﹣d)的值为( )
A.9 B.﹣16 C.25 D.﹣25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com