
分析 (1)先求出两车半小时行驶70km,再乘以4可求甲乙两地之间相距的距离;
(2)先求出两车的速度和,再根据相遇时快车比慢车多行驶40km,可得快车比慢车的速度快40÷2=20km/小时,依此可求快车和慢车行驶的速度;
(3)设快车出发x小时,两车相距35km,分四种情况:①两车相遇前,相距35km,②两车相遇后,相距35km,③快车到达乙地后,慢车到达甲地前,相距35km,④慢车到达甲地后,相距35km,进行讨论即可求解.
解答 解:(1)70÷(2-1.5)×2
=70÷0.5×2
=280(km).
答:甲乙两地之间相距280km;
(2)(280÷2+40÷2)÷2
=160÷2
=80(km/h),
(280÷2-40÷2)÷2
=120÷2
=60(km/h),
故快车行驶的速度80 km/h,慢车行驶的速度60km/h.
(3)设快车出发x小时,两车相距35km,
①两车相遇前,相距35km,
则有80x+35+60x=280,解得x=$\frac{7}{4}$;
②两车相遇后,相距35km,
则有80x-35+60x=280,解得x=$\frac{9}{4}$;
③快车到达乙地后,慢车到达甲地前,相距35km,
则有80x-280+35=60x,解得x=$\frac{49}{4}$,
因为慢车走完全程需要$\frac{14}{3}$小时,$\frac{49}{4}$>$\frac{14}{3}$,
所以不合题意,舍去;
④慢车到达甲地后,相距35km,
则有80x+35=280×2,解得x=$\frac{105}{16}$
综上所述,$\frac{7}{4}$小时或$\frac{9}{4}$小时或$\frac{105}{16}$小时,两车相距35km.
故答案为:280.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意分类思想的应用.


科目:初中数学 来源: 题型:解答题
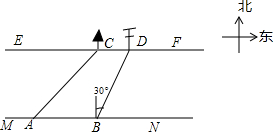 在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com