
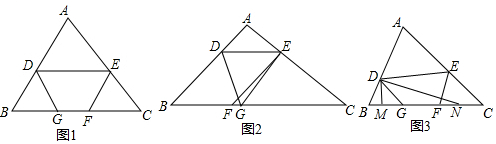
 在△ABC,∠1=∠2,∠3=∠4,∠5=∠6,∠A=60°,求∠ECF,∠F的度数.
在△ABC,∠1=∠2,∠3=∠4,∠5=∠6,∠A=60°,求∠ECF,∠F的度数. 分析 先根据∠3=∠4,∠5=∠6,求得∠ECF=∠3+∠5=$\frac{1}{2}$×180°=90°即可,再根据∠ACD是△ABC的外角,∠6是△BCF的外角,即可求得∠F=$\frac{1}{2}$∠ACD-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$×∠A.
解答 解:∵∠3=∠4,∠5=∠6,
∴∠ECF=∠3+∠5=$\frac{1}{2}$∠ACB+$\frac{1}{2}$∠ACD=$\frac{1}{2}$×180°=90°.
∵∠ACD是△ABC的外角,
∴∠A=∠ACD-∠ABC,
∵∠6是△BCF的外角,
∴∠F=∠6-∠2,
又∵∠1=∠2,∠5=∠6,
∴∠F=$\frac{1}{2}$∠ACD-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$×∠A=30°.
点评 本题主要考查了三角形的外角性质以及三角形内角和定理的运用,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
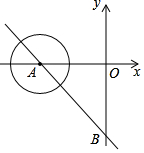 如图,在直角坐标系中直线AB分别交x轴,y轴与A(-6,0)、B(0,-8)两点,现有一半径为1的动圆,圆心由A点,沿着AB方向以每秒1个单位的速度做平移运动,则经过几秒后动圆与坐标轴相切.
如图,在直角坐标系中直线AB分别交x轴,y轴与A(-6,0)、B(0,-8)两点,现有一半径为1的动圆,圆心由A点,沿着AB方向以每秒1个单位的速度做平移运动,则经过几秒后动圆与坐标轴相切.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com