
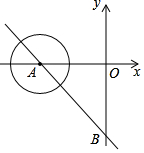
 如图,在直角坐标系中直线AB分别交x轴,y轴与A(-6,0)、B(0,-8)两点,现有一半径为1的动圆,圆心由A点,沿着AB方向以每秒1个单位的速度做平移运动,则经过几秒后动圆与坐标轴相切.
如图,在直角坐标系中直线AB分别交x轴,y轴与A(-6,0)、B(0,-8)两点,现有一半径为1的动圆,圆心由A点,沿着AB方向以每秒1个单位的速度做平移运动,则经过几秒后动圆与坐标轴相切. 分析 在直角三角形OAB中,OA=6,OB=8,由勾股定理得AB=10,设⊙经过t秒后与坐标轴相切,
(1)当⊙经过t秒后到达P点与x轴相切,过P点作x轴的垂线,垂足为D,则PD=1,由△APD∽△ABO中的成比例线段求解;
(2)当⊙经过t秒后到达K点与y轴相切,过k点作y轴的垂线,垂足为E,则KE=1,KB=10-t;由△KEB∽△ABO中的成比例线段求解;
(3)当⊙经过t秒后到达Q点与y轴相切,过q点作y轴的垂线,垂足为c,则QC=1,BQ=t-10,由△QBC∽△ABO中的成比例线段求解;
解答 解:∵A(-6,0)、B(0,-8)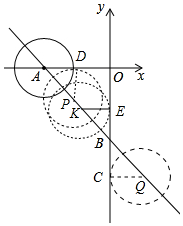
∴OA=6,OB=8,
∴AB=10,
(1)当⊙经过t秒后到达P点与x轴相切,过P点作x轴的垂线,垂足为D,则PD=1;
由△APD∽△ABO得,$\frac{AP}{AB}$=$\frac{PD}{OB}$,即$\frac{t}{10}$=$\frac{1}{8}$,
解得t=$\frac{5}{4}$;
(2)当⊙经过t秒后到达K点与y轴相切,过k点作y轴的垂线,垂足为E,则KE=1;KB=10-t;
由△KEB∽△ABO得,$\frac{KB}{AB}$=$\frac{KE}{OA}$,即$\frac{10-t}{10}$=$\frac{1}{6}$,
解得t=$\frac{25}{3}$.
(3)当⊙经过t秒后到达Q点与y轴相切,过q点作y轴的垂线,垂足为c,则QC=1;BQ=t-10,
由△QBC∽△ABO得,$\frac{BQ}{AB}$=$\frac{CQ}{OA}$,即$\frac{t-10}{10}$=$\frac{1}{6}$,解得t=$\frac{35}{3}$,
综上所述,t=$\frac{5}{4}$s或$\frac{25}{3}$s或$\frac{35}{3}$s时,动圆与坐标轴相切.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
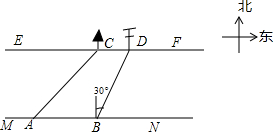 在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com