Question

12．如图所示，在三角形ABC中，G为BC上一动点，∠DBF=∠DEF，∠BDG=∠BGD，DG平分∠BDE．
（1）如图①，当G点在BF上时，求证：BD∥EF；
（2）如图②，当G在CF上时，连接GE，若∠DEG=3∠FEG，∠DGE=60°，则∠CGE的度数为45°；
（3）如图③，在（1）的条件下，若DM平分∠BDG，交BC于点M，DN平分∠ADM，交BC于点N，若∠BND=15°，求∠B的度数．

Answer 1

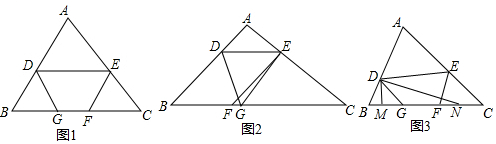
分析 （1）先判定DE∥BG，得出∠B+∠BDE=180°，再根据∠B=∠DEF，得到∠DEF+∠BDE=180°，进而得出BD∥EF；
（2）设∠FEG=α，则∠DEG=3∠FEG=3α，∠DEF=2α=∠B，根据DE∥BC，得到∠DGB=∠EDG=120°-3α=∠BDG，再根据△DBG中，∠B+∠BDG+∠BGD=180°，列出方程2α+（120°-3α）+（120°-3α）=180°，解得α=15°，最后根据DE∥BC，求得∠CGE=∠DEF=45°即可；
（3）设∠B=β，根据DE∥BC，得到∠ADE=β，∠EDN=∠BND=15°，∠ADN=β+15°，再根据DN平分∠ADM，求得∠MDN=β+15°，根据等腰三角形的性质，得到∠BDG=∠BGD=$\frac{180°-∠B}{2}$=90°-$\frac{1}{2}$β，而DM平分∠BDG，进而得到∠DMN=∠BDM+∠B=45°-$\frac{1}{4}$β+β=45°+$\frac{3}{4}$β，最后根据△MDN中，∠MDN+∠DMN+∠DNM=180°，列出方程（β+15°）+（45°+$\frac{3}{4}$β）+15°=180°，解得β=60°即可．

解答 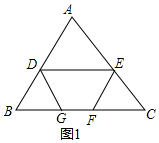解：（1）∵∠BDG=∠BGD，DG平分∠BDE，
∴∠BGD=∠EDG，
∴DE∥BG，
∴∠B+∠BDE=180°，
又∵∠B=∠DEF，
∴∠DEF+∠BDE=180°，
∴BD∥EF；

（2）设∠FEG=α，则∠DEG=3∠FEG=3α，∠DEF=2α=∠B，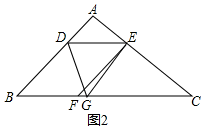
∵∠DGE=60°，
∴△DEG中，∠EDG=180°-3α-60°=120°-3α，
∵DE∥BC，
∴∠DGB=∠EDG=120°-3α=∠BDG，
∵△DBG中，∠B+∠BDG+∠BGD=180°，
2α+（120°-3α）+（120°-3α）=180°，
解得α=15°，
∴∠DEG=45°，
∵DE∥BC，
∴∠CGE=∠DEF=45°，
故答案为：45°；

（3）设∠B=β，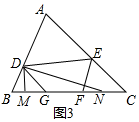
∵DE∥BC，
∴∠ADE=β，∠EDN=∠BND=15°，
∴∠ADN=β+15°，
∵DN平分∠ADM，
∴∠MDN=β+15°，
又∵△BDG中，∠BDG=∠BGD=$\frac{180°-∠B}{2}$=90°-$\frac{1}{2}$β，而DM平分∠BDG，
∴∠BDM=$\frac{1}{2}$∠BDG=45°-$\frac{1}{4}$β，
∴∠DMN=∠BDM+∠B=45°-$\frac{1}{4}$β+β=45°+$\frac{3}{4}$β，
∵△MDN中，∠MDN+∠DMN+∠DNM=180°，
∴（β+15°）+（45°+$\frac{3}{4}$β）+15°=180°，
解得β=60°，
∴∠B的度数为60°．

点评 本题属于三角形综合题，主要考查了平行线的判定与性质、三角形内角和定理、角平分线的定义的综合应用，解决问题的关键是根据三角形内角和等于180°，列出方程进行求解．解题时注意方程思想的灵活运用．