
分析 (1)(2)(3)应用加法交换律和加法结合律,求出算式的值是多少即可.
(4)应用平方差公式和完全平方公式,求出算式的值是多少即可.
解答 解:(1)3$\sqrt{3}$-$\sqrt{8}$+$\sqrt{2}$-$\sqrt{27}$
=3$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{2}$-3$\sqrt{3}$
=(3$\sqrt{3}$-3$\sqrt{3}$)+(-2$\sqrt{2}$+$\sqrt{2}$)
=0-$\sqrt{2}$
=-$\sqrt{2}$
(2)|$\sqrt{3}$-2|+(-$\frac{1}{2}$)0+$\frac{1}{{\sqrt{3}}$-$\sqrt{48}$
=2-$\sqrt{3}$+1+$\frac{\sqrt{3}}{3}$-4$\sqrt{3}$
=(-$\sqrt{3}$+$\frac{\sqrt{3}}{3}$-4$\sqrt{3}$)+(2+1)
=3-$\frac{14}{3}$$\sqrt{3}$
(3)$\sqrt{8}$+3$\sqrt{\frac{1}{3}$-$\frac{1}{{\sqrt{2}}$+$\frac{{\sqrt{3}}}{2}$
=2$\sqrt{2}$+$\sqrt{3}$-$\frac{\sqrt{2}}{2}$+$\frac{{\sqrt{3}}}{2}$
=(2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$)+($\sqrt{3}$+$\frac{{\sqrt{3}}}{2}$)
=$\frac{3}{2}\sqrt{2}$+$\frac{3}{2}$$\sqrt{3}$
(4)($\sqrt{7}$+$\sqrt{5}$+$\sqrt{3}$)($\sqrt{7}$-$\sqrt{5}$-$\sqrt{3}$)
=${(\sqrt{7})}^{2}$-${(\sqrt{5}+\sqrt{3})}^{2}$
=7-(8+2$\sqrt{15}$)
=-1-2$\sqrt{15}$
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
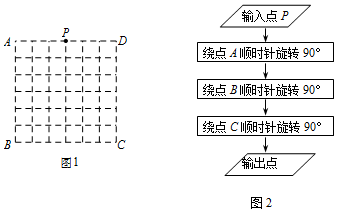
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
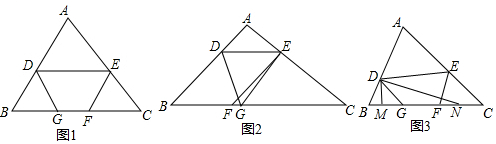
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com