
 OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.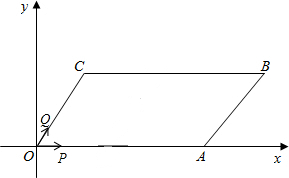
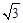 ),OB=4
),OB=4 cm(2)
cm(2) ,当t=8时,S最大(3)a=1+
,当t=8时,S最大(3)a=1+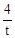 (0<t≤8)或a=1-
(0<t≤8)或a=1- (6≤t≤8)
(6≤t≤8)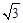 ),OB=4
),OB=4 cm。
cm。 
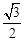 t。
t。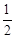 OP·QD=
OP·QD= t2。
t2。
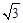 。
。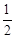 DP·QE=
DP·QE=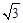 t。
t。 
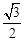 (t-8)。
(t-8)。 =
=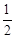 t·2
t·2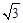 -
-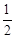 t·
t·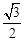 (t-8)
(t-8) t2+3
t2+3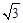 t。
t。  。
。
 ,S随t的增加而减小,
,S随t的增加而减小,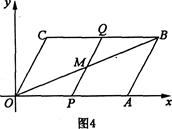
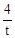 。 t的取值范围是0<t≤8。
。 t的取值范围是0<t≤8。 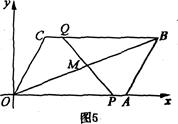
 , 即
, 即 。∴OM=
。∴OM= 。
。  ,即
,即 。
。 ,t的取值范围是6≤t≤8。
,t的取值范围是6≤t≤8。 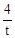 (0<t≤8)或a=1-
(0<t≤8)或a=1- (6≤t≤8)。
(6≤t≤8)。 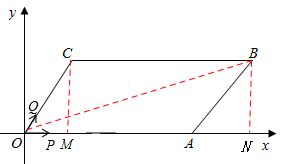
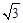 ,
,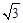 )。
)。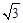 ,
, 。
。

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
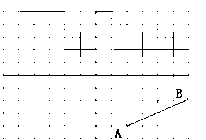
 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题: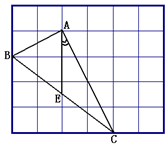
 的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 .
的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 .查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
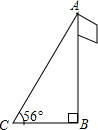
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com