
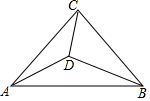
 如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.
如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.分析 (1)只要证明∠CDA=135°,∠ADB=135°即可解决问题.
(2)根据两角对应相等两三角形相似即可判定.
(3)由△DCA∽△DAB,推出$\frac{DC}{DA}$=$\frac{DA}{DB}$=$\frac{AC}{BA}$=$\frac{1}{\sqrt{2}}$,又CD=1,推出AD=$\sqrt{2}$,DB=2.根据BC=$\sqrt{C{D}^{2}+B{D}^{2}}$,求出BC,再在Rt△ABC中,求出AB即可解决问题.
解答 (1)解:∵△ABC为等腰直角三角形,
∴∠CAB=45°.
又∵∠ACD=∠DAB,
∴∠ACD+∠CAD=∠DAB+∠CAD=∠CAB=45°,
∴∠CDA=135°
同理可得∠ADB=135°
∴∠CDB=360°-∠CDA-∠ADB=360°-135°-135°=90°.
(2)证明:∵∠CDA=∠ADB,∠ACD=∠DAB,
∴△DCA∽△DAB
(3)解:∵△DCA∽△DAB,
∴$\frac{DC}{DA}$=$\frac{DA}{DB}$=$\frac{AC}{BA}$=$\frac{1}{\sqrt{2}}$,
又∵CD=1,
∴AD=$\sqrt{2}$,DB=2.
又∵∠CDB=90°,
∴BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
在Rt△ABC中,∵AC=BC=$\sqrt{5}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{10}$.
点评 本题考查相似三角形的判定和性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,本题的突破点是发现∠CDB=90°,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )| A. | (0,42015) | B. | (0,42014) | C. | (0,32015) | D. | (0,32014) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
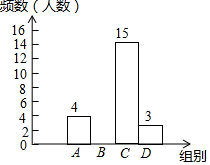 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题. | 组别 | 成绩x(分) | 频数(人数) |
| A | 8.0≤x<8.5 | a |
| B | 8.5≤x<9.0 | 8 |
| C | 9.0≤x<9.5 | 15 |
| D | 9.5≤x<10 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
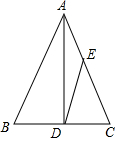 如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com