
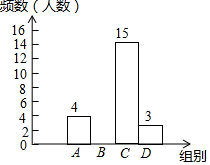
 Ϊ�ḻѧ����У���ijУ���С��밮ͬ�С����б�����������������ͬѧ�ijɼ������Ƴ����²�������ͳ��ͼ���������ͼ���е���Ϣ����������⣮
Ϊ�ḻѧ����У���ijУ���С��밮ͬ�С����б�����������������ͬѧ�ijɼ������Ƴ����²�������ͳ��ͼ���������ͼ���е���Ϣ����������⣮ | ��� | �ɼ�x���֣� | Ƶ���������� |
| A | 8.0��x��8.5 | a |
| B | 8.5��x��9.0 | 8 |
| C | 9.0��x��9.5 | 15 |
| D | 9.5��x��10 | 3 |
���� ��1��������ͼ�ɵ�a��ֵ�����������Ķ��弰Ƶ���ֲ����ɵô𰸣�
��2������Ƶ���ֲ����ó�B���Ƶ�����ɲ�ȫ����ͼ��
��3���б����ó����еȿ��ܽ�����ٸ��ݸ��ʹ�ʽ�ɵô𰸣�
��� �⣺��1��������ͳ��ͼ��֪��a=4����Ƶ���ֲ�ֱ��ͼ��֪��α����ɼ�����������C�飬
�ʴ�Ϊ��4��C��
��2����ȫƵ���ֲ�ֱ��ͼ���£�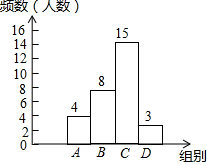
��3����������ɫ���·ֱ��Ϊ��1����2��������״ͼ�����б��� �ã�
| ��1 | ��2 | �� | |
| �� | ����1���ڣ� | ����2���ڣ� | �������ڣ� |
| �� | ����1������ | ����2������ | ���������� |
| �� | ����1���ף� | ����2���ף� | �������ף� |
���� ���⿼����Ƶ���ֲ���������ͳ��ͼ������ͳ��ͼ�����߶γ��ȱ�ʾ���ݣ����������Ķ��ٻ��ɳ��̲�ͬ�ľ���ֱ����Ȼ��˳�����Щֱ������������������ͼ���Ժ����������ݵĴ�С�����ڱȽϣ�Ҳ����������ͳ��ͼ�б�������״ͼ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
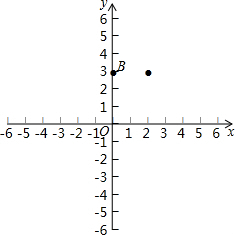 ��֪������y=ax2+bx+c�Ķ���ΪA��������B��0��3���͵㣨2��3������x�ύ��C��D���㣬����C�ڵ�D����ࣩ����OD=OB��
��֪������y=ax2+bx+c�Ķ���ΪA��������B��0��3���͵㣨2��3������x�ύ��C��D���㣬����C�ڵ�D����ࣩ����OD=OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
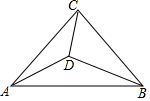 ��ͼ���ڵ���ֱ�ǡ�ABC�У���ACB=90�㣬��DΪ��������һ�㣬�ҡ�ACD=��DAB=��DBC��
��ͼ���ڵ���ֱ�ǡ�ABC�У���ACB=90�㣬��DΪ��������һ�㣬�ҡ�ACD=��DAB=��DBC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com