
”¾ĢāÄæ”æÄ³ÖŠŃ§æŖÕ¹”°Ńō¹āĢåÓżŅ»Š”Ź±”±»ī¶Æ£¬°“ѧŠ£Źµ¼ŹĒéæö£¬¾ö¶ØæŖÉčA£ŗĢßė¦×Ó£»B£ŗĄŗĒņ£»C£ŗĢųÉž£»D£ŗĘ¹ÅŅĒņĖÄÖÖŌĖ¶ÆĻīÄ棬ĪŖĮĖ½āѧɜ×īĻ²»¶ÄÄŅ»ÖÖŌĖ¶ÆĻīÄ棬Ė껜³éČ”ĮĖŅ»²æ·Öѧɜ½ųŠŠµ÷²é£¬¾®½«µ÷²é½į¹ū»ęÖĘ³ÉČēĻĀĮ½øöĶ³¼ĘĶ¼£®Ēė½įŗĻĶ¼ÖŠµÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£®

£Ø1£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬”°B”±ĖłŌŚÉČŠĪµÄŌ²ŠÄ½ĒŹĒ¶ąÉŁ¶Č£æ£»
£Ø2£©½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©ČōøĆ֊ѧӊ1200Ćūѧɜ£¬Ļ²»¶ĄŗĒņŌĖ¶ÆµÄѧɜŌ¼ÓŠ¶ąÉŁĆū£æ
”¾“š°ø”æ£Ø1£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬”°B”±ĖłŌŚÉČŠĪµÄŌ²ŠÄ½ĒŹĒ54”ć£»£Ø2£©²¹Č«Ķ¼ŠĪ¼ū½āĪö£»£Ø3£©Ļ²»¶ĄŗĒņŌĖ¶ÆµÄѧɜŌ¼ÓŠ180Ćū£®
”¾½āĪö”æ
£Ø1£©ĻČĒóBĻīÄæ¶ŌÓ¦µÄ°Ł·Ö±Č£¬ŌŁ³ĖŅŌ360”ć¼“æÉ£»
£Ø2£©ĻČ¼ĘĖć±»µ÷²éµÄ×ÜČĖŹż£¬ŌŁ¼ĘĖćCĻīÄæµÄČĖŹż£¬Č»ŗó²¹Č«Ķ³¼ĘĶ¼£»
£Ø3£©øł¾ŻŃł±¾¹Ą¼Ę×ÜĢ壬ÓĆøĆ֊ѧµÄѧɜ×ÜŹż1200³ĖŅŌ×īĻ²»¶ĄŗĒņŌĖ¶ÆĻīÄæĖłÕ¼µÄ°Ł·Ö±Č¼“æÉ.
½ā£ŗ£Ø1£©”ßBĻīÄæ¶ŌÓ¦µÄ°Ł·Ö±ČĪŖ1©£Ø40%+20%+25%£©£½15%£¬
”ąŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬”°B”±ĖłŌŚÉČŠĪµÄŌ²ŠÄ½ĒŹĒ360”ć”Į15%£½54”ć£»
£Ø2£©”ß±»µ÷²éµÄ×ÜČĖŹżĪŖ80”Ā40%£½200£ØČĖ£©£¬
”ąCĻīÄæµÄČĖŹżĪŖ200©£Ø80+30+50£©£½40£ØČĖ£©£¬
²¹Č«Ķ¼ŠĪČēĻĀ£ŗ
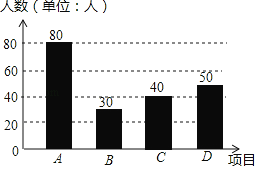
£Ø3£©ČōøĆ֊ѧӊ1200Ćūѧɜ£¬ŌņĻ²»¶ĄŗĒņŌĖ¶ÆµÄѧɜŌ¼ÓŠ1200”Į15%£½180£ØĆū£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ķ¼¢ŁŹĒŅ»øöĖıߊĪÖ½Ģõ ABCD£¬ĘäÖŠ AB”ĪCD£¬E£¬F ·Ö±šĪŖ±ß AB£¬CD ÉĻµÄĮ½øöµć£¬½«Ö½Ģõ ABCD ŃŲ EF ÕŪµžµĆµ½Ķ¼¢Ś£¬ŌŁ½«Ķ¼¢ŚŃŲ DF ÕŪµžµĆµ½Ķ¼¢Ū£¬ČōŌŚĶ¼¢ŪÖŠ£¬”ĻFEM=26”ć£¬Ōņ”ĻEFC µÄ¶ČŹżĪŖ£Ø £©

A.52”ćB.64”ćC.102”ćD.128”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮ²ÄĮĻ£ŗ¶ŌÓŚ£Øx©1£©£Øx©3£©£¾0£¬ÕāĄą²»µČŹ½£¬ĪŅĆĒæÉŅŌ½ųŠŠĻĀĆęµÄ½āĢāĖ¼Ā·ÓÉÓŠĄķŹżµÄ³Ė·Ø·ØŌņ”°Į½ŹżĻą³Ė£¬Ķ¬ŗŵĆÕż”±£¬æÉµĆ£Ø1£©![]() »ņ£Ø2£©
»ņ£Ø2£©![]() “Ó¶ų½«Ī“ÖŖµÄŅ»ŌŖ¶ž“Ī²»µČŹ½×Ŗ»ÆĪŖѧ¹żµÄŅ»ŌŖŅ»“Ī²»µČŹ½×飬·Ö±š½āÕāĮ½øö²»µČŹ½×飬¼“æÉĒóµĆŌ²»µČŹ½µÄ½ā¼Æ£¬¼“£ŗ½ā²»µČŹ½×é£Ø1£©µĆx£¾3£¬½ā²»µČŹ½×é£Ø2£©µĆx£¼1£¬ĖłŅŌ£Øx©1£©£Øx©3£©£¾0µÄ½ā¼ÆĪŖx£¾3»ņx£¼1£®
“Ó¶ų½«Ī“ÖŖµÄŅ»ŌŖ¶ž“Ī²»µČŹ½×Ŗ»ÆĪŖѧ¹żµÄŅ»ŌŖŅ»“Ī²»µČŹ½×飬·Ö±š½āÕāĮ½øö²»µČŹ½×飬¼“æÉĒóµĆŌ²»µČŹ½µÄ½ā¼Æ£¬¼“£ŗ½ā²»µČŹ½×é£Ø1£©µĆx£¾3£¬½ā²»µČŹ½×é£Ø2£©µĆx£¼1£¬ĖłŅŌ£Øx©1£©£Øx©3£©£¾0µÄ½ā¼ÆĪŖx£¾3»ņx£¼1£®
Ēėøł¾ŻŅŌÉĻ²ÄĮĻ»Ų“šĻĀĆęĪŹĢā£ŗ
£Ø1£©Ö±½ÓŠ“³ö£Øx©2£©£Øx©5£©£¼0µÄ½ā¼Æ£»
£Ø2£©·ĀÕÕÉĻŹö²ÄĮĻ£¬Ēó![]() £¾0µÄ½ā¼Æ£®
£¾0µÄ½ā¼Æ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø±¾ĢāĀś·Ö8·Ö£©ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻDACŹĒ”÷ABCµÄŅ»øöĶā½Ē£®
Źµ¼łÓė²Ł×÷£ŗ
øł¾ŻŅŖĒó³ß¹ę×÷Ķ¼£¬²¢ŌŚĶ¼ÖŠ±źĆ÷ĻąÓ¦×ÖÄø£Ø±£Įō×÷Ķ¼ŗŪ¼££¬²»Š“×÷·Ø£©£®

£Ø1£©×÷”ĻDACµÄĘ½·ÖĻßAM£»
£Ø2£©×÷Ļ߶ĪACµÄ“¹Ö±Ę½·ÖĻߣ¬ÓėAM½»ÓŚµćF£¬ÓėBC±ß½»ÓŚµćE£¬Į¬½ÓAE”¢CF£®
²ĀĻė²¢Ö¤Ć÷£ŗ
ÅŠ¶ĻĖıߊĪAECFµÄŠĪד²¢¼ÓŅŌÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AC£¬BDĻą½»ÓŚµćO£¬AEĘ½·Ö”ĻBAD½»BCÓŚµćE£¬Čō”ĻCAE£½15”ć£¬Ōņ”ĻBOEµÄ¶ČŹżĪŖ____________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĶ¬Ń§ÉĻѧʌµÄŹżŃ§Ąś“Ī²āŃé³É¼ØČēĻĀ±ķĖłŹ¾£ŗ
²āŃ饹±š | Ę½Ź±²āŃé | ĘŚÖŠ²āŃé | ĘŚÄ©²āŃé | ||
µŚ1“Ī | µŚ2“Ī | µŚ3“Ī | |||
³É¼Ø | 100 | 106 | 106 | 105 | 110 |
£Ø1£©øĆĶ¬Ń§ÉĻѧʌ5“Ī²āŃé³É¼ØµÄÖŚŹżĪŖ £¬ÖŠĪ»ŹżĪŖ £»
£Ø2£©øĆĶ¬Ń§ÉĻѧʌŹżŃ§Ę½Ź±³É¼ØµÄĘ½¾łŹżĪŖ £»
£Ø3£©øĆĶ¬Ń§ÉĻѧʌµÄ×Ü³É¼ØŹĒ½«Ę½Ź±²āŃéµÄĘ½¾ł³É¼Ø”¢ĘŚÖŠ²āŃé³É¼Ø”¢ĘŚÄ©²āŃé³É¼Ø°“ÕÕ2£ŗ3£ŗ5µÄ±ČĄż¼ĘĖćĖłµĆ£¬ĒóøĆĶ¬Ń§ÉĻѧʌŹżŃ§Ń§æʵÄ×ÜĘĄ³É¼Ø£Ø½į¹ū±£ĮōÕūŹż£©”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļß![]() ¹żĘ½ŠŠĖıߊĪ
¹żĘ½ŠŠĖıߊĪ![]() ¶Ō½ĒĻߵĽ»µć
¶Ō½ĒĻߵĽ»µć![]() £¬·Ö±š½»
£¬·Ö±š½»![]() ”¢
”¢![]() ÓŚ
ÓŚ![]() ”¢
”¢![]() £¬ÄĒĆ“ŅõÓ°²æ·ÖµÄĆ껿ŹĒĘ½ŠŠĖıߊĪ
£¬ÄĒĆ“ŅõÓ°²æ·ÖµÄĆ껿ŹĒĘ½ŠŠĖıߊĪ![]() Ć껿µÄ(”” ””)
Ć껿µÄ(”” ””)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]() £Ø
£Ø![]() ĪŖ·ĒĮć³£Źż£©£®
ĪŖ·ĒĮć³£Źż£©£®
£Ø![]() £©Čō¶Ō³ĘÖįŹĒÖ±Ļß
£©Čō¶Ō³ĘÖįŹĒÖ±Ļß![]() £®
£®
¢ŁĒ󶞓ĪŗÆŹżµÄ½āĪöŹ½£®
¢Ś¶ž“ĪŗÆŹż![]() £Ø
£Ø![]() ĪŖŹµŹż£©Ķ¼ĻóµÄ¶„µćŌŚ
ĪŖŹµŹż£©Ķ¼ĻóµÄ¶„µćŌŚ![]() ÖįÉĻ£¬Ēó
ÖįÉĻ£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
£Ø![]() £©°ŃÅ×ĪļĻß
£©°ŃÅ×ĪļĻß![]() ĻņÉĻĘ½ŅĘ
ĻņÉĻĘ½ŅĘ![]() øöµ„Ī»µĆµ½ŠĀµÄÅ×ĪļĻß
øöµ„Ī»µĆµ½ŠĀµÄÅ×ĪļĻß![]() £¬Čō
£¬Čō![]() £¬Ēó
£¬Ēó![]() µÄĶ¼ĻńĀäŌŚ
µÄĶ¼ĻńĀäŌŚ![]() ÖįÉĻ·½µÄ²æ·Ö¶ŌÓ¦µÄ
ÖįÉĻ·½µÄ²æ·Ö¶ŌÓ¦µÄ![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĻ߶Ī![]() £¬
£¬ ![]() ÓŚµć
ÓŚµć![]() £¬ĒŅ
£¬ĒŅ![]() £¬
£¬ ![]() ŹĒÉäĻß
ŹĒÉäĻß![]() ÉĻŅ»¶Æµć£¬
ÉĻŅ»¶Æµć£¬ ![]() ”¢
”¢![]() ·Ö±šŹĒ
·Ö±šŹĒ![]() £¬
£¬ ![]() µÄÖŠµć£¬¹żµć
µÄÖŠµć£¬¹żµć![]() £¬
£¬ ![]() £¬
£¬ ![]() µÄŌ²Óė
µÄŌ²Óė![]() µÄĮķŅ»½»µć
µÄĮķŅ»½»µć![]() £Øµć
£Øµć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻ£©£¬Į¬½į
ÉĻ£©£¬Į¬½į![]() £¬
£¬ ![]() £®
£®

£Ø![]() £©µ±
£©µ±![]() Ź±£¬Ōņ
Ź±£¬Ōņ![]() µÄ¶ČŹżĪŖ__________£®
µÄ¶ČŹżĪŖ__________£®
£Ø![]() £©ŌŚµć
£©ŌŚµć![]() µÄŌĖ¶Æ¹ż³ĢÖŠ£¬µ±
µÄŌĖ¶Æ¹ż³ĢÖŠ£¬µ±![]() Ź±£¬Č”ĖıߊĪ
Ź±£¬Č”ĖıߊĪ![]() Ņ»±ßµÄĮ½¶ĖµćŗĶĻ߶Ī
Ņ»±ßµÄĮ½¶ĖµćŗĶĻ߶Ī![]() ÉĻŅ»µć
ÉĻŅ»µć![]() £¬ČōŅŌÕāČżµćĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£¬µ±
£¬ČōŅŌÕāČżµćĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£¬µ±![]() Ź±£¬Ōņ
Ź±£¬Ōņ![]() µÄÖµĪŖ__________£®
µÄÖµĪŖ__________£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com