
【题目】如图,等边△ABC的边长为6,点O是三边垂直平分线的交点,∠FOG=120°,∠FOG的两边OF,OG分别交AB,BC与点D,E,∠FOG绕点O顺时针旋转时,下列四个结论正确的是( )

①OD=OE;②![]() ;③
;③![]() ;④△BDE的周长最小值为9,
;④△BDE的周长最小值为9,
A.1个B.2个C.3个D.4个
【答案】B
【解析】
连接OB、OC,如图,利用等边三角形的性质得∠ABO=∠OBC=∠OCB=30°,再证明∠BOD=∠COE,于是可判断△BOD≌△COE,所以BD=CE,OD=OE,则可对①进行判断;利用S△BOD=S△COE得到四边形ODBE的面积=![]() S△ABC=
S△ABC=![]() ,则可对③进行判断;作OH⊥DE,如图,则DH=EH,计算出S△ODE=
,则可对③进行判断;作OH⊥DE,如图,则DH=EH,计算出S△ODE=![]() OE2,利用S△ODE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断;由于△BDE的周长=BC+DE=6+DE=
OE2,利用S△ODE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断;由于△BDE的周长=BC+DE=6+DE=![]() OE,根据垂线段最短,当OE⊥BC时,OE最小,△BDE的周长最小,计算出此时OE的长则可对④进行判断.
OE,根据垂线段最短,当OE⊥BC时,OE最小,△BDE的周长最小,计算出此时OE的长则可对④进行判断.
解:连接OB、OC,如图,

∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵点O是等边△ABC的内心,
∴OB=OC,OB、OC分别平分∠ABC和∠ACB,
∴∠ABO=∠OBC=∠OCB=30°,
∴∠BOC=120°,即∠BOE+∠COE=120°,
而∠DOE=120°,即∠BOE+∠BOD=120°,
∴∠BOD=∠COE,
在△BOD和△COE中,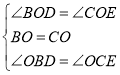 ,
,
∴△BOD≌△COE(ASA),
∴BD=CE,OD=OE,①正确;
∴S△BOD=S△COE,
∴四边形ODBE的面积=S△OBC=![]() S△ABC=
S△ABC=![]() ×
×![]() ×62=
×62=![]() ,③错误
,③错误
作OH⊥DE,如图,则DH=EH,
∵∠DOE=120°,
∴∠ODE=∠OEH=30°,
∴OH=![]() OE,HE=
OE,HE=![]() OH=
OH=![]() OE,
OE,
∴DE=![]() OE,
OE,
∴S△ODE=![]()
![]() OE
OE![]() OE=
OE=![]() OE2,
OE2,
即S△ODE随OE的变化而变化,
而四边形ODBE的面积为定值,
∴S△ODE≠S△BDE;②错误;
∵BD=CE,
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=6+DE=6+![]() OE,
OE,
当OE⊥BC时,OE最小,△BDE的周长最小,此时OE=![]() ,
,
∴△BDE周长的最小值=6+3=9,④正确.
故选:B.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】在数学活动课上,某活动小组用棋子摆出了下列图形:
![]()


 ……
……
第1个图形 第2个图形 第3个图形 第4个图形
(1)探索新知:
①第![]() 个图形需要_________枚棋子;②第
个图形需要_________枚棋子;②第![]() 个图形需要__________枚棋子.
个图形需要__________枚棋子.
(2)思维拓展:
小明说:“我要用![]() 枚棋子摆出一个符合以上规律的图形”,你认为小明能摆出吗?如果能摆出,请问摆出的是第几个图形;如果不能,请说明理由.
枚棋子摆出一个符合以上规律的图形”,你认为小明能摆出吗?如果能摆出,请问摆出的是第几个图形;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,把表示数1的点称为基准点,记作点![]() .对于两个不同的点M和N,若点M、点N到点
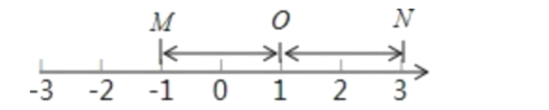
.对于两个不同的点M和N,若点M、点N到点![]() 的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点
的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点![]() 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b=_________;若a=4,则b=_________;
②用含a的式子表示b,则b=____________;
(2)对点A进行如下操作:先把点A表示的数乘以2.5,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是___________;
(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,…,依此顺序不断地重复,得到
的基准变换点,…,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .
.![]() 为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
,![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,…,依此顺序不断地重复,得到
,…,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .若无论k为何值,
.若无论k为何值,![]() 与
与![]() 两点间的距离都是4,则n=__________
两点间的距离都是4,则n=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个有两个圆柱形构成的容器,最下面的圆柱形底面半径![]() 。匀速地向空容器内注水,水面高度
。匀速地向空容器内注水,水面高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:小时)的关系如图2所示。
(单位:小时)的关系如图2所示。

(1)求水面高度![]() 与时间
与时间![]() 的函数关系式;
的函数关系式;
(2)求注水的速度(单位:立方米/每小时),并求容器内水的体积![]() 与注水时间
与注水时间![]() 的函数关系式;
的函数关系式;
(3)求上面圆柱的底面半径(壁厚忽略不计)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工程队承包了地铁某标段全长3900米的施工任务,分别从南,北两个方向同时向前掘进。已知甲工程队比乙工程队平均每天多掘进0.4米经过13天的施工两个工程队共掘进了156米.
(1)求甲,乙两个工程队平均每天各掘进多少米?
(2)为加快工程进度两工程队都改进了施工技术,在剩余的工程中,甲工程队平均每天能比原来多掘进0.4米,乙工程队平均每天能比原来多掘进0.6米,按此施工进度能够比原来少用多少天完成任务呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=BC=5,AC=6,△ABC沿BC方向向右平移得△DCE,A、C对应点分别是D、E.AC与BD相交于点O.
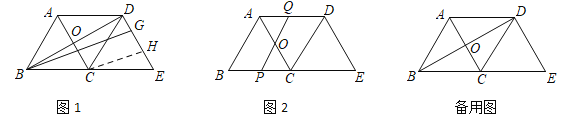
(1)将射线BD绕B点顺时针旋转,且与DC,DE分别相交于F,G,CH∥BG交DE于H,当DF=CF时,求DG的长;
(2)如图2,将直线BD绕点O逆时针旋转,与线段AD,BC分别相交于点Q,P.设OQ=x,四边形ABPQ的周长为y,求y与x之间的函数关系式,并求y的最小值.
(3)在(2)中PQ的旋转过程中,△AOQ是否构成等腰三角形?若能构成等腰三角形,求出此时PQ的长?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长![]() (单位长度)。慢车长
(单位长度)。慢车长![]() (单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点
(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点![]() 为原点,取向右方向为正方向画数轴,此时快车
为原点,取向右方向为正方向画数轴,此时快车![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,慢车头
,慢车头![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,若快车
,若快车![]() 以
以![]() 个单位长度/秒的速度向右匀速继续行驶,同时慢车
个单位长度/秒的速度向右匀速继续行驶,同时慢车![]() 以
以![]() 个单位长度/秒的速度向左匀速继续行驶,且
个单位长度/秒的速度向左匀速继续行驶,且![]() 与
与![]() 互为相反数.
互为相反数.
(1)求此时刻快车头![]() 与慢车头
与慢车头![]() 之间相距多少单位长度?
之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒两列火车行驶到车头![]() 、
、![]() 相距
相距![]() 个单位长度?
个单位长度?
(3)此时在快车![]() 上有一位爱到脑筋的七年级学生乘客
上有一位爱到脑筋的七年级学生乘客![]() ,他发现行驶中有一段时间,他的位置
,他发现行驶中有一段时间,他的位置![]() 到两列火车头
到两列火车头![]() 、
、![]() 的距离和加上到两列火车尾
的距离和加上到两列火车尾![]() 、
、![]() 的距离和是一个不变的值(即
的距离和是一个不变的值(即![]() 为定值),你认为学生
为定值),你认为学生![]() 发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.
发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.
![]()
附加题:
查看答案和解析>>
科目:初中数学 来源: 题型:
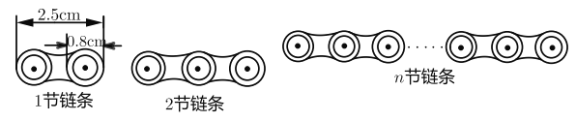
【题目】如图,自行车链条每节链条的长度为2.5cm ,交叉重叠部分的圆的直径为0.8cm.
(1)尝试: 2节链条总长度是________ ![]() , 3节链条总长度是________
, 3节链条总长度是________ ![]() .
.
(2)发现:用含![]() 的代数式表示
的代数式表示![]() 节链条总长度是________. ( 要求填写最简结果)
节链条总长度是________. ( 要求填写最简结果)
(3)应用:如果某种型号自行车链条总长度为![]() ,则它是由多少节这样的链条构成的?
,则它是由多少节这样的链条构成的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com