
【题目】某中学在今年4月23日的“世界读书日”开展“人人喜爱阅读,争当阅读能手”活动,同学们积极响应,涌现出大批的阅读能手.为了激励同学们的阅读热情,养成每天阅读的好习惯,学校对阅读能手进行了奖励表彰,计划用2700元来购买甲、乙、丙三种书籍共100本作为奖品,已知甲、乙、丙三种书的价格比为2:2:3,甲种书每本20元.
(1)求出乙、丙两种书的每本各多少元?
(2)若学校购买甲种书的数量是乙种书的1.5倍,恰好用完计划资金,求甲、乙、丙三种书各买了多少本?
(3)在活动中,同学们表现优秀,学校决定提升奖励档次,增加了245元的购书款,在购买书籍总数不变的情况下,求丙种书最多可以买多少本?
(4)七(1)班阅读氛围浓厚,同伴之间交换书籍共享阅读,已知甲种书籍共270页,小明同学阅读甲种书籍每天21页,阅读5天后,发现同伴比他看得快,为了和同伴及时交换书籍,接下来小明每天多读了a页(20<a<40),结果再用了b天读完,求小明读完整本书共用了多少天?
【答案】(1)乙、丙每本分别是20元、30元;(2)甲乙丙三种书分别购买了18本、12本、70本;(3)m最大值是94本(4)共用了8天、或9天.
【解析】
(1)由甲、乙、丙三种书的价格比为2:2:3,且甲种书每本20元可得;
(2)设乙买了x本,丙买了y本,则甲买了1.5x本,根据“甲、乙、丙三种书籍共100本、共用用2700元”列方程组求解可得;
(3)设丙种书可以买m本,由购书总钱数不超过2945列不等式求解可得;
(4)根据(5+b)天读大于等于270和20<a<40确定b的范围,再根据b是整数来求解.
解:(1)因为甲、乙、丙三种书的价格比为2:2:3,甲种书每本20元.
所以乙、丙每本分别是20元、30元;
(2)设乙买了x本,丙买了y本,则甲买了1.5x本,
根据题意得![]() ,
,
解得![]() ,
,
则甲是1.5x=1.5×12=18,
答:甲乙丙三种书分别购买了18本、12本、70本;
(3)设丙种书可以买m本,
则20(100-m)+30m≤2945,
解得m≤94.5,
因为m是正整数,
所以m最大值是94本.
(4)∵21×5+(21+a)b≥270,
∴b≥![]() ,
,
∵20<a<40,
∴![]() <b<
<b<![]() ,
,
∴b=3、4,
所以共用了8天、或9天.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠ADC= 度;
(2)当∠C=20°时,判断DE与AC的位置关系,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层。第二层……第n层,第n层的小正方体的个数记为S.解答下列问题:
(1)填写表格:
n | 1 | 2 | 3 | 4 | … |
S | 1 |
| … |
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
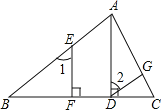
求证:DG∥BA.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=90°,∠ADB=90°(______)
∴∠EFB=∠ADB(等量代换)
∴EF∥AD(______)
∴∠1=∠BAD(______)
又∵∠1=∠2(已知)
∴∠______=∠______(等量代换)
∴DG∥BA.(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 落在平行四边形
落在平行四边形![]() 所在平面内,
所在平面内,![]() 和
和![]() 相交于点
相交于点![]() ,连接
,连接![]()
![]() 判断
判断![]() 和
和![]() 的位置关系,并证明.
的位置关系,并证明.
![]() 在图1中,若
在图1中,若![]() ,是否存在
,是否存在![]() 恰好为直角三角形的情形?若存在,求出
恰好为直角三角形的情形?若存在,求出![]() 的长度:若不存在,请说明理由.
的长度:若不存在,请说明理由.
![]() 若将图中平行四边形纸片
若将图中平行四边形纸片![]() 换成矩形纸片
换成矩形纸片![]() ,沿对角线折叠发现所得图形是轴对称图形;将所得图形沿其对称轴再次折叠后,得到的仍是轴对称图形.则矩形纸片
,沿对角线折叠发现所得图形是轴对称图形;将所得图形沿其对称轴再次折叠后,得到的仍是轴对称图形.则矩形纸片![]() 的长宽之比是多少?请直接写出结果.
的长宽之比是多少?请直接写出结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣ ![]() )2=
)2= ![]()
D.3x2﹣4x﹣2=0化为(x﹣ ![]() )2=
)2= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一蚂蚁从A点出发,沿着A→B→C→D→A…循环爬行,其中A点的坐标为(2,﹣2),B点的坐标为(﹣2,﹣2),C点的坐标为(﹣2,6),D点的坐标为(2,6),当蚂蚁爬了2018个单位时,蚂蚁所处位置的坐标为( )

A. (﹣2,0)B. (4,﹣2)C. (﹣2,4)D. (0,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com