
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠ADC= 度;
(2)当∠C=20°时,判断DE与AC的位置关系,并说明理由。

【答案】(1)80;(2)DE∥AC,理由见解析.
【解析】
(1)根据三角形一个外角等于它不相邻两个内角之和,即可得出答案;
(2)由∠ADC=80°,可以求得∠ADB=100°,由△ABD沿AD折叠得到△AED,可得∠ADE=∠ADB=100°,继而根据三角形外角的性质可求得∠EDF=20°,继而可得∠EDF=∠C,从而可得DE∥AC.
(1)∠ADC=∠B+∠BAD=50°+30°=80°,
故答案为:80;
(2)DE∥AC,理由如下:
∵∠B=50°,∠BAD=30°,
∴∠ADC=50°+30°=80°,
∴∠ADB=180°-∠ADC=100°,
∵△ABD沿AD折叠得到△AED,
∴∠ADE=∠ADB=100°,
∴∠EDF=∠ADE -∠ADF=100°-80°=20°,
又∵∠C=20°,
∴∠EDF=∠C,
∴DE∥AC.


科目:初中数学 来源: 题型:
【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节,一场新冠病毒疫情由武汉开始席卷了整个中华地区,全国人民齐心协力、共同抗疫.为了防止感染,![]() 口罩成为了大众纷纷抢购的必需品,由于需求增加导致价格不断走高,引起了民众与政府的高度关注,据统计:2020年2月份一盒
口罩成为了大众纷纷抢购的必需品,由于需求增加导致价格不断走高,引起了民众与政府的高度关注,据统计:2020年2月份一盒![]() 口罩价格比2020年1月份上涨了
口罩价格比2020年1月份上涨了![]() ,某市民2020年2月3日在某超市订购了一盒
,某市民2020年2月3日在某超市订购了一盒![]() 口罩花了52元.
口罩花了52元.
(1)问:2020年1月份一盒![]() 口罩的价格为多少元?
口罩的价格为多少元?
(2)某超市将进货价为每盒39元的![]() 口罩,按2020年2月3日价格出售,平均一天能销售出100盒,经调查表明:
口罩,按2020年2月3日价格出售,平均一天能销售出100盒,经调查表明:![]() 口罩的售价每盒下降1元,其口罩销售量就增加10盒,超市为了实现销售
口罩的售价每盒下降1元,其口罩销售量就增加10盒,超市为了实现销售![]() 口罩每天有1320元的利润,并且尽可能让顾客得到实惠,每盒
口罩每天有1320元的利润,并且尽可能让顾客得到实惠,每盒![]() 口罩的售价应该下降多少元?
口罩的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 中,在
中,在![]() 边上取两点
边上取两点![]() 、
、![]() ,使
,使![]() .若
.若![]() ,
,![]() ,
,![]() , 则以
, 则以![]() ,
,![]() ,
,![]() 为边长的三角形的形状为( )
为边长的三角形的形状为( )

A.锐角三角形B.直角三角形C.钝角三角形D.随![]() ,
,![]() ,
,![]() 的值而定
的值而定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
(1)四边形AFBE是矩形;
(2)MN=![]() BC.
BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形中的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……,按此规律第5个图中共有点的个数是( )

A. 31 B. 46 C. 51 D. 66
查看答案和解析>>
科目:初中数学 来源: 题型:
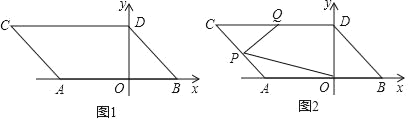
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|2a+6|+(2a﹣3b+12)2=0,现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)请直接写出A,B两点的坐标;
(2)如图2,点P是线段AC上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段AC上移动时(不与A,C重合),请找出∠PQD,∠OPQ,∠POB的数量关系,并证明你的结论;
(3)在坐标轴上是否存在点M,使三角形MAD的面积与三角形ACD的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在今年4月23日的“世界读书日”开展“人人喜爱阅读,争当阅读能手”活动,同学们积极响应,涌现出大批的阅读能手.为了激励同学们的阅读热情,养成每天阅读的好习惯,学校对阅读能手进行了奖励表彰,计划用2700元来购买甲、乙、丙三种书籍共100本作为奖品,已知甲、乙、丙三种书的价格比为2:2:3,甲种书每本20元.
(1)求出乙、丙两种书的每本各多少元?
(2)若学校购买甲种书的数量是乙种书的1.5倍,恰好用完计划资金,求甲、乙、丙三种书各买了多少本?
(3)在活动中,同学们表现优秀,学校决定提升奖励档次,增加了245元的购书款,在购买书籍总数不变的情况下,求丙种书最多可以买多少本?
(4)七(1)班阅读氛围浓厚,同伴之间交换书籍共享阅读,已知甲种书籍共270页,小明同学阅读甲种书籍每天21页,阅读5天后,发现同伴比他看得快,为了和同伴及时交换书籍,接下来小明每天多读了a页(20<a<40),结果再用了b天读完,求小明读完整本书共用了多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com