
【题目】已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
(1)四边形AFBE是矩形;
(2)MN=![]() BC.
BC.
【答案】证明:(1)∵BE、BF分别是△ABC中∠B及它的外角的平分线,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∵AE⊥BE,E为垂足,AF⊥BF,F为垂足,
∴∠AFB=∠AEB=90°,
∴四边形AEBF为矩形;
(2)∵四边形AEBF为矩形,
∴BM=MA=ME,
∴∠2=∠5,
∵∠2=∠1,
∴∠1=∠5,
∴ME∥BC,
∵M是AB的中点,
∴N为AC的中点,
∴MN=![]() BC.
BC.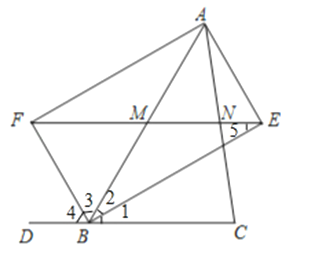
【解析】(1)由BE、BE是角平分线可得∠EBF是90°,进而由条件中的两个垂直可得两个直角,可得四边形AEBF是矩形;
(2)由矩形的F质可得∠2=∠5进而利用角平分线的性质可得∠1=∠5,可得ME∥BC,进而可得N为AC中点,根据三角形中位线性质求出即可.
【考点精析】本题主要考查了三角形中位线定理的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】为鼓励市民节约用电,小亮家所在地区规定:每户居民如果一个月的用电量不超过![]() 度,那么这户居民这个月只需交
度,那么这户居民这个月只需交![]() 元电费;如果超过
元电费;如果超过![]() 度,则这个月除了仍要交
度,则这个月除了仍要交![]() 元的电费以外,超过的部分还要按每度
元的电费以外,超过的部分还要按每度![]() 元交电费.已知小亮家
元交电费.已知小亮家![]() 月份用电
月份用电![]() 度,交电费
度,交电费![]() 元;
元;![]() 月份用电
月份用电![]() 度,交电费
度,交电费![]() 元.
元.
(1)请直接写出小亮家![]() 月份超过
月份超过![]() 度部分的用电量(用含
度部分的用电量(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同的小正方体堆成的一个几何体,如图所示.

(1)请画出这个几何体的三视图;
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 ________个正方体只有一个面是黄色,有 __________个正方体只有两个面是黄色,有 ________个正方体只有三个面是黄色.
(3)若现在你手头还有一些相同的小正方体,如果保持图的几何体的俯视图和左视图不变,最多可以再添加几个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,点D,E分别在边AB, BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=80°,则∠EGC的度数为( )。

A. 70°B. 75°C. 80°D. 85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠ADC= 度;
(2)当∠C=20°时,判断DE与AC的位置关系,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE. 
(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
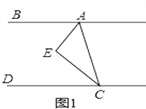
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com