
����Ŀ��ij��˾��2014�꿪ʼͶ�뼼���Ľ��ʽ𣬾������Ľ������Ʒ�ijɱ����Ͻ��ͣ������������±���
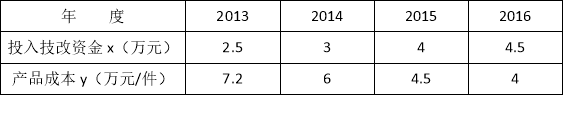
��1��������������������ݣ���һ�κ����ͷ�����������ȷ����һ�������ܱ�ʾ��仯���ɣ��������ɣ�����������ʽ��
��2���������ֱ仯���ɣ���2017����Ͷ���ʽ�5��Ԫ��
��Ԥ�������ɱ�ÿ����2016�꽵�Ͷ�����Ԫ��
����������2017���ÿ����Ʒ�ɱ����͵�3.2��Ԫ������ҪͶ�뼼���ʽ������Ԫ���������ȷ��0.01��Ԫ����
���𰸡���1��![]() ����2����0.4����1.13��
����2����0.4����1.13��
��������
�����������1������ʵ������������ص�������⣬�����ų�����֪��Ϊ���������������ô���ϵ������⼴�ɣ�
��2����ֱ�Ӱ�x=5��Ԫ���뺯������ʽ������⣻
��ֱ�Ӱ�y=3.2��Ԫ���뺯������ʽ������⣻
�����������1������Ϊһ�κ���������ʽΪy=kx+b����x=2.5ʱ��y=7.2����x=3ʱ��y=6����![]() �����k=��2.4��b=13.2����һ�κ�������ʽΪy=��2.4x+13.2��
�����k=��2.4��b=13.2����һ�κ�������ʽΪy=��2.4x+13.2��
��x=4ʱ��y=4.5����˺�������ʽ��������ұߣ����䲻��һ�κ�����
ͬ������Ҳ���Ƕ��κ�����
����Ϊ����������������ʽΪ![]() ��
��
��x=2.5ʱ��y=7.2���ɵã�7.2=![]() �����k=18
�����k=18
��������������![]() ��
��
��֤����x=3ʱ��y=![]() =6�����Ϸ�����������
=6�����Ϸ�����������
ͬ������֤x=4ʱ��y=4.5��x=4.5ʱ��y=4������
���÷���������![]() ��ʾ��仯���ɣ�
��ʾ��仯���ɣ�
��2������x=5��Ԫʱ��y=3.6��
4��3.6=0.4����Ԫ�����������ɱ�ÿ����2009�꽵��0.4��Ԫ��
����y=3.2��Ԫʱ��3.2=![]() ����x=5.625����5.625��4.5=1.125��1.13����Ԫ��
����x=5.625����5.625��4.5=1.125��1.13����Ԫ��
����Լ��Ͷ��1.13��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У���B���C��ƽ���߽��ڵ�P�� 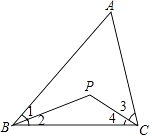
��1������A=112��ʱ�����BPC�Ķ�����
��2������A=��ʱ�����BPC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����в��ϲ��ش����⣺
�ڽ��ʽ���� ![]() ʱ��С���Ľⷨ���£�
ʱ��С���Ľⷨ���£�
�⣺��������ͬ���ԣ�x+1����x��1������2��x��1����3=1��
ȥ���ţ���2x��1=3��1 ��
���x= ![]()
���飺��x= ![]() ʱ����x+1����x��1����0 ��
ʱ����x+1����x��1����0 ��
����x= ![]() ��ԭ��ʽ���̵Ľ� ��
��ԭ��ʽ���̵Ľ� ��
��1������ΪС������������˴�����ֻ����ţ�
��2�����С�����ʽ���̳��ֵĴ���ͽ��ʽ�����е�������Ҫ���裬��������������ʽ����ʱ��ע�����
��3��д��������ʽ���̵���ȷ�ⷨ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ӵ�ˮ���ٶ���5km/h�����ھ�ˮ�е��ٶ���vkm/h��������ˮ��ʻ�е��ٶ���_____km/h��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��999��1001
��2��2015+20152��2015��2016
��3��[a2+b2+2b��a��b������a��b��2]��4b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ɶ������Կ�ͨ��������չ�ٶȲ��ϼӿ죬���ѳ�Ϊ�ɶ�������Ҫ���з�ʽ֮һ������4��29�ճɶ�������ȫ����˿�Լ181��˴Σ���һ��ˢ�¿�����¼����Ҳ�ǽ����������Ĵο�����¼��ˢ�£��ÿ�ѧ��������ʾ181��Ϊ�� ��
A.18.1��105
B.1.81��106
C.1.81��107
D.181��104
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ��������У���ƻ������ס������ֹ����������¹�����ͼ�飬���鷢�֣�������������3�����������2���������ʽ�1020Ԫ��������������4�����������3���������ʽ�1440Ԫ��
��1���ס����������ÿ���ļ۸�ֱ��Ƕ���Ԫ��
��2������У�ƻ����������ֹ������20�������������������������ڼ�������������ѧУ�����ܹ��ṩ�ʽ�4320Ԫ������Ƽ��ֹ��������ѧУѡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ڴ��з���290��Ϳ�к졢�ڡ���������ɫ���ʵ���ͬ��С������������Ǻ��������2����40�����Ӵ�����ȡһ�����ǰ���ĸ�����![]() ��
��
��1������к���ĸ�����
��2����Ӵ�����ȡһ�����Ǻ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и���|��2|��������2��2��������2��������2��3�У������ĸ����У�������
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com