
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.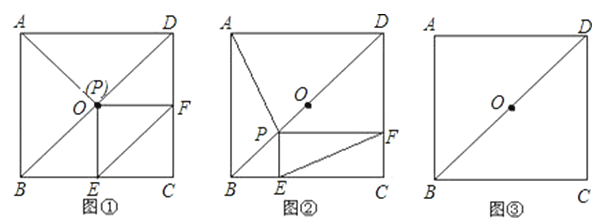
【答案】解:(1)AP=EF,AP⊥EF,理由如下:
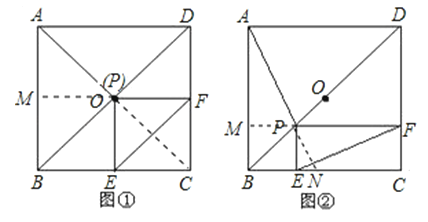
连接AC,则AC必过点O,延长FO交AB于M;
∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,
∴四边形OECF是正方形,
∴OM=OF=OE=AM,
∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,
∴△AMO≌△FOE(AAS),
∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,
故AP=EF,且AP⊥EF.
(2)题(1)的结论仍然成立,理由如下:
延长AP交BC于N,延长FP交AB于M;
∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,
∴四边形MBEP是正方形,
∴MP=PE,∠AMP=∠FPE=90°;
又∵AB﹣BM=AM,BC﹣BE=EC=PF,且AB=BC,BM=BE,
∴AM=PF,
∴△AMP≌△FPE(SAS),
∴AP=EF,∠APM=∠FPN=∠PEF
∵∠PEF+∠PFE=90°,∠FPN=∠PEF,
∴∠FPN+∠PFE=90°,即AP⊥EF,
故AP=EF,且AP⊥EF.
(3)题(1)(2)的结论仍然成立;
如右图,延长AB交PF于H,证法与(2)完全相同.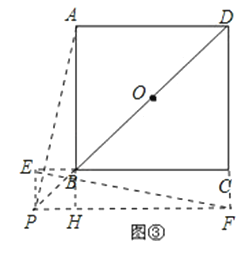
【解析】(1)连接AC,则AC必过O点,延长FO交AB于M,由于O是BD中点,易证得△AOM≌△FOE,则AO=EF,且∠AOM=∠FOC=∠OFE=45°,由此可证得AP⊥EF.
(2)方法与①类似,延长FP交AB于M,延长AP交BC于N,易证得四边形MBEP是正方形,可证得△APM≌△FEP,则AP=EF,∠APM=∠FEP;而∠APM=∠FPN=∠PEF,且∠PEF与∠PFE互余,故∠PFE+∠FPN=90°,由此可证得AP⊥EF,所以(1)题的结论仍然成立.
(3)解题思路和方法同(2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某水资源保护组织对邢台某小区的居民进行节约水资源的问卷调查.某居民在问卷的选项代号上画“√”,这个过程是收集数据中的( )
A. 确定调查范围B. 汇总调查数据
C. 实施调查D. 明确调查问题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边彤OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )

A. 10 B. 9 C. 8 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.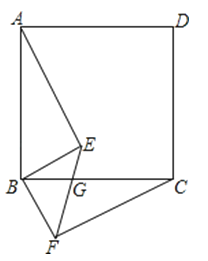
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在楼AB与楼CD之间有一旗杆EF,从AB顶部A点处经过旗杆顶部E点恰好看到楼CD的底部D点,且俯角为45°,从楼CD顶部C点处经过旗杆顶部E点恰好看到楼AB的G点,BG=1米,且俯角为30°,己知楼AB高20米,求旗杆EF的高度.(结果精确到1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k≠0,x<0)的图象过等边三角形AOB的顶点A(﹣1,
(k≠0,x<0)的图象过等边三角形AOB的顶点A(﹣1,![]() ),已知点B在x轴上.
),已知点B在x轴上.
(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图象上,需将△AOB向上平移多少个单位长度?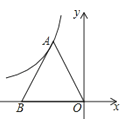
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品安全问题已经严重影响到我们的健康.某执法部门最近就食品安全抽样调查某一家超市,从中随机抽样选取20种包装食品,并列出下表:
食品质量 | 优 | 良 | 合格 | 不合格 | 有害或有毒食品 |
数量 | 0 | 2 | 3 | n | 4 |
请你根据以上信息解答下列问题:
(1)这次抽样调查中,“食品质量为合格以上(含合格)”的频率为多少?
(2)若这家超市经销的包装食品共有1300种,请你估计大约有多少种包装食品是“有害或有毒”的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4![]() ,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,
,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF, ![]() 经过点C,则图中阴影部分的面积为( )
经过点C,则图中阴影部分的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com